题目内容
8.如图,△ABC中,BD⊥AC于D,E为BD上一点,且∠ABD=38°,∠CBD=68°,∠BCE=14°,∠DCE=8°,求∠DAE的度数.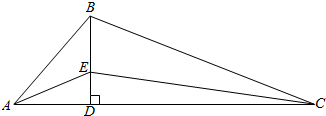
分析 设∠DAE=α,由已知可得CD:AD=tanα:tan8°=tan52°:tan22°,利用两角和与差的正切公式,及正切的三倍角公式,诱导公式,可得答案.
解答 解:∵△ABC中,BD⊥AC于D,E为BD上一点,且∠ABD=38°,∠CBD=68°,∠BCE=14°,∠DCE=8°,
设∠DAE=α,
则DE=tan8°•CD=tanα•AD,BD=tan(14°+8°)•CD=tan(90°-38°)•AD,
即tan8°•CD=tanα•AD,tan22°•CD=tan52°•AD,
∴CD:AD=tanα:tan8°=tan52°:tan22°,
tanα=$\frac{tan52°•tan8°}{tan22°}$=$\frac{tan(30°+22°)•tan(30°-22°)}{tan22°}$=$\frac{\frac{\frac{1}{3}-{tan}^{2}22°}{1-\frac{1}{3}{tan}^{2}22°}}{tan22°}$=$\frac{\frac{1}{3}-{tan}^{2}22°}{tan22°-\frac{1}{3}{tan}^{3}22°}$=$\frac{1}{\frac{tan22°-\frac{1}{3}{tan}^{3}22°}{\frac{1}{3}-{tan}^{2}22°}}$=$\frac{1}{\frac{3tan22°-{tan}^{3}22°}{1-3{tan}^{2}22°}}$=$\frac{1}{tan(3×22°)}$=cot66°=tan24°,
∴α=24°
点评 本题考查的知识点是两角和与差的正切公式,及正切的三倍角公式,诱导公式,本题难度较大.

练习册系列答案
相关题目
18.$f(x)=\left\{\begin{array}{l}{(3-a)x+1\\;x<1}\\{{a}^{x}\\;x≥1}\end{array}\right.$,满足对任意x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0成立,那么a的取值范围是( )
| A. | (1,3) | B. | (1,2] | C. | [2,3) | D. | (1,+∞) |
16.为了对某课题进行研究,用分层抽样的方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见表(单位:人)
(Ⅰ)求x,y;
(Ⅱ)若从高校B、C抽取的人中选2人作专题发言,求这2人都来自高校C的概率.
| 高校 | 相关人数 | 抽取人数 |
| A | 15 | 1 |
| B | 30 | x |
| C | 60 | y |
(Ⅱ)若从高校B、C抽取的人中选2人作专题发言,求这2人都来自高校C的概率.
13.点P(-1,2,3)关于zOx平面对称的点的坐标是( )
| A. | (1,2,3) | B. | (-1,-2,3) | C. | (-1,2,-3) | D. | (1,-2,-3) |
17.函数f(x)=x3+x-1在下列哪个区间内有零点?( )
| A. | (-1,0) | B. | (1,2) | C. | (0,1) | D. | (2,3) |