题目内容
函数 的部分图象如图所示,则将y=f(x)的图象向右平移
的部分图象如图所示,则将y=f(x)的图象向右平移 单位后,得到的图象解析式为 .
单位后,得到的图象解析式为 .
【答案】分析:由图知,A=1, T=
T= π,可求ω,再由
π,可求ω,再由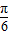 ω+φ=
ω+φ=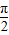 可求得φ,从而可得y=f(x)的解析式,利用y=Asin(ωx+φ)的图象变换及可求得答案.
可求得φ,从而可得y=f(x)的解析式,利用y=Asin(ωx+φ)的图象变换及可求得答案.
解答:解:由图知,A=1, T=
T= π,
π,
∴T=π,ω=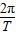 =2,又
=2,又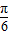 ×2+φ=
×2+φ=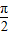 +2kπ(k∈Z),
+2kπ(k∈Z),
∴φ=2kπ+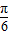 (k∈Z),又|φ|<
(k∈Z),又|φ|<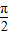 ,
,
∴φ=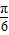 ;
;
∴y=f(x)的解析式为y=sin(2x+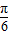 ),
),
∴将y=f(x)的图象向右平移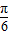 单位后得y=sin[2(x-
单位后得y=sin[2(x-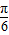 )+
)+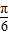 ]=sin(2x-
]=sin(2x-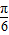 ).
).
故答案为:y=sin(2x-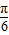 ).
).
点评:本题考查y=Asin(ωx+φ)的部分图象确定函数解析式,考查函数y=Asin(ωx+φ)的图象变换,考查识图与运算能力,属于中档题.
 T=
T= π,可求ω,再由
π,可求ω,再由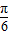 ω+φ=
ω+φ=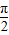 可求得φ,从而可得y=f(x)的解析式,利用y=Asin(ωx+φ)的图象变换及可求得答案.
可求得φ,从而可得y=f(x)的解析式,利用y=Asin(ωx+φ)的图象变换及可求得答案.解答:解:由图知,A=1,
 T=
T= π,
π,∴T=π,ω=
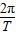 =2,又
=2,又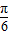 ×2+φ=
×2+φ=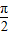 +2kπ(k∈Z),
+2kπ(k∈Z),∴φ=2kπ+
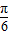 (k∈Z),又|φ|<
(k∈Z),又|φ|<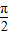 ,
,∴φ=
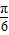 ;
;∴y=f(x)的解析式为y=sin(2x+
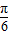 ),
),∴将y=f(x)的图象向右平移
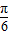 单位后得y=sin[2(x-
单位后得y=sin[2(x-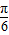 )+
)+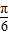 ]=sin(2x-
]=sin(2x-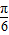 ).
).故答案为:y=sin(2x-
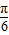 ).
).点评:本题考查y=Asin(ωx+φ)的部分图象确定函数解析式,考查函数y=Asin(ωx+φ)的图象变换,考查识图与运算能力,属于中档题.

练习册系列答案
相关题目
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( )
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( ) 已知函数f(x)是(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )
已知函数f(x)是(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( ) (2012•福州模拟)函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为4
(2012•福州模拟)函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为4 (2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( )
(2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( ) 函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,该函数的部分图象如图所示,A、B分别为最高点与最低点,并且
函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,该函数的部分图象如图所示,A、B分别为最高点与最低点,并且