题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,满足bcosC=(4a-c)cosB.
(I)求cosB;
(Ⅱ)若b=
,S△ABC=
,求a,c的值.
(I)求cosB;
(Ⅱ)若b=
| 34 |
3
| ||
| 2 |
考点:正弦定理
专题:解三角形
分析:(1)由正弦定理化简已知得sinBcosC=(4sinA-sinC)cosB,化简得sin(B+C)=sinA=4sinAcosB,由0<A<π,sinA≠0,即可求得cosB.
(2)由(1)可得sinB,由S△ABC=
acsinB=
,可解得ac,由余弦定理可解得:a2+b2=40.从而解得a,c的值.
(2)由(1)可得sinB,由S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
解答:
解:(1)由正弦定理可得:sinBcosC=(4sinA-sinC)cosB,
化简可得:sinBcosC-sinCcosB,
可得:sin(B+C)=sinA=4sinAcosB,
因为:0<A<π,sinA≠0,
所以:cosB=
.
(2)∵sinB=
=
,
∵S△ABC=
acsinB=
,
∴可解得:ac=12,
∴由余弦定理可得:cosB=
=
=
.可解得:a2+b2=40.
∴可解得:a+c=8,从而解得:a=2或6,c=6或2.
化简可得:sinBcosC-sinCcosB,
可得:sin(B+C)=sinA=4sinAcosB,
因为:0<A<π,sinA≠0,
所以:cosB=
| 1 |
| 4 |
(2)∵sinB=
| 1-cos2B |
| ||
| 4 |
∵S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
∴可解得:ac=12,
∴由余弦定理可得:cosB=
| a2+c2-b2 |
| 2ac |
| 1 |
| 4 |
| a2+c2-34 |
| 2ac |
∴可解得:a+c=8,从而解得:a=2或6,c=6或2.
点评:本题主要考查了正弦定理,余弦定理,三角形面积公式的应用,考查了两角和的正弦公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
设集合A={x||x|<1},B={x|log2x≤0},则A∩B=( )
| A、{x|-1<x<1} |
| B、{x|0<x<1} |
| C、{x|-1<x≤1} |
| D、{x|0<x≤1} |
函数f(x)=
的递增区间为( )
| x2-4x |
| A、[2,+∞) |
| B、[4,+∞) |
| C、(-∞,2] |
| D、(-∞,4] |
在一个△ABC中,若a=2,b=2,A=30°,那么B等于( )
| A、60° |
| B、60°或 120° |
| C、30° |
| D、30°或150° |
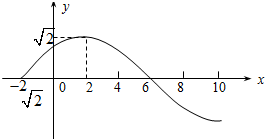 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<