题目内容
已知圆C: ,直线
,直线
(Ⅰ)求证:对任意 ,直线
,直线 与圆C总有两个不同交点;
与圆C总有两个不同交点;
(Ⅱ)设 与圆C交于A、B两点,若|AB|=
与圆C交于A、B两点,若|AB|= ,求直线
,求直线 的倾斜角
的倾斜角 ;
;
(Ⅲ)求弦AB的中点M的轨迹方程.
【答案】
(1)证明:由已知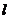 :
: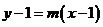 可得,直线
可得,直线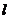 过定点
过定点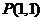
∵12+()=1<5,
∴点P在圆C内,故直线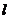 与圆C总有两个不同交点.
与圆C总有两个不同交点.
(2)圆心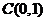 到直线的距离d=
到直线的距离d=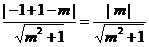 ,
而|AB|=
,
而|AB|=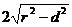 .
.
又|AB|=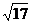 ,∴
,∴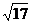 =
=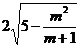 .
解得m=
.
解得m=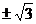 ,
,
∴直线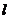 的倾斜角为α=60°或α=120°.
的倾斜角为α=60°或α=120°.
(3)设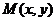 ,连结CM、CP,其中
,连结CM、CP,其中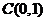 ,
,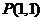 ,
,
∵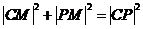 ,∴
,∴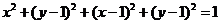
整理得点M的轨迹方程为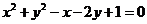

练习册系列答案
相关题目