题目内容
已知函数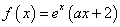 (
(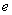 为自然对数的底数,
为自然对数的底数,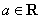 为常数).对于函数
为常数).对于函数 ,若存在常数
,若存在常数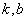 ,对于任意
,对于任意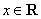 ,不等式
,不等式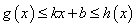 都成立,则称直线
都成立,则称直线 是函数
是函数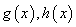 的分界线.
的分界线.
(I)若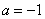 ,求
,求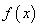 的极值;
的极值;
(II)讨论函数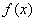 的单调性;
的单调性;
(III)设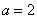 ,试探究函数
,试探究函数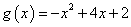 与函数
与函数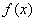 是否存在“分界线”?若存在,求出分界线方程;若不存在,试说明理由.
是否存在“分界线”?若存在,求出分界线方程;若不存在,试说明理由.
解:(I)若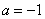 ,则
,则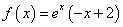 ,
,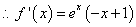 ,
,
由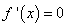 得
得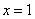 ,又
,又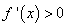 得
得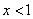 ;
; 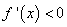 得
得 ,
,
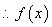 在
在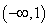 单调递增,在
单调递增,在 单调递减;
单调递减;
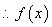 在
在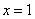 处取得极大值
处取得极大值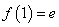 ,无极小值.
,无极小值.
(II)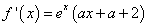 ,
,
①当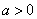 时,由
时,由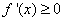 得
得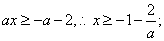
由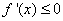 得
得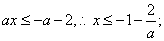
函数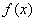 在区间
在区间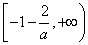 上是增函数,在区间
上是增函数,在区间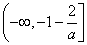 上是减函数:
上是减函数:
②当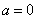 时,
时,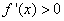 对
对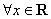 恒成立,此时函数
恒成立,此时函数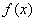 是区间
是区间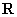 上的增函数;
上的增函数;
③当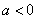 时,由
时,由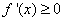 得
得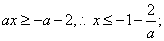
由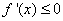 得
得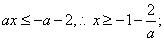
函数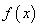 在区间
在区间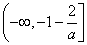 上是增函数,在区间
上是增函数,在区间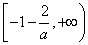 上是减函数.
上是减函数.
(III)若存在,则 恒成立,
恒成立,
令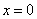 ,则
,则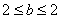 ,所以
,所以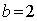 ,
,
因此: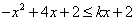 对
对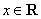 恒成立,即
恒成立,即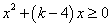 对
对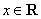 恒成立,
恒成立,
由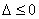 得到
得到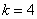 , 现在只要判断
, 现在只要判断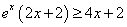 是否恒成立,
是否恒成立,
设 ,则
,则 ,
,
①当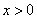 时,
时,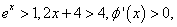
②当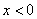 时,
时,
所以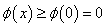 ,即
,即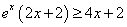 恒成立,
恒成立,
所以函数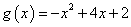 与函数
与函数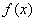 存在“分界线”,且方程为
存在“分界线”,且方程为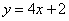

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
对甲、乙两名自行车赛手在相同条件下进行了8次测试,测得他们的最大速度(单位:m/s)的数据如下表:
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 | 24 | 50 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 | 43 | 45 |
(1)画出茎叶图,由茎叶图你能获得哪些信息?
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)的数据的平均数、中位数、标准差,并判断选谁参加比赛更合适(可用计算器).
 (其中
(其中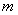 为整数),则
为整数),则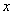 最近的整数,记作
最近的整数,记作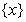 ,即
,即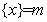 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数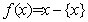 的四个判断:
的四个判断: 的定义域是
的定义域是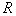 ,值域是
,值域是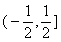 ;
;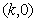 是
是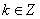 ;
;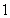 ;
;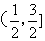 上是增函数.
上是增函数.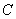 与圆
与圆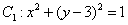 和圆
和圆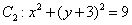 都外切,则动圆圆心
都外切,则动圆圆心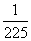 B.
B.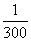 C.
C.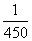 D.以上全不对
D.以上全不对 B.
B.  C.
C.  D.
D. 

 与圆C:
与圆C: 相交于A、B两点,则
相交于A、B两点,则 的值为 ___ .
的值为 ___ .  ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 在[0,3]上的最大值和最小值分别是( )
在[0,3]上的最大值和最小值分别是( )  C. 5,
C. 5, D. 5,
D. 5,