题目内容
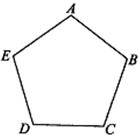 15、如图,正五边形ABCDE中,若把顶点A、B、C、D、E染上红、黄、绿、三种颜色中的一种,使得相邻顶点所染颜色不相同,则不同的染色方法共有
15、如图,正五边形ABCDE中,若把顶点A、B、C、D、E染上红、黄、绿、三种颜色中的一种,使得相邻顶点所染颜色不相同,则不同的染色方法共有
30
种.分析:由题意知给五个定点染色,使得相邻顶点所染颜色不相同,可以将图中五个点分成三组,每一组可以用三种颜色全排列,分组时,要用两对不相邻的定点还有一个单独的点组成,得到结果.
解答:解:由题意知给五个定点染色,使得相邻顶点所染颜色不相同
将图中五个点分成三组:AC、BD、E;
AC、BE、D;
AD、BE、C;
AD、CE、B;
BD、CE、A.共五种情况,
于是有5A33=30种涂色方法.
故答案为:30.
将图中五个点分成三组:AC、BD、E;
AC、BE、D;
AD、BE、C;
AD、CE、B;
BD、CE、A.共五种情况,
于是有5A33=30种涂色方法.
故答案为:30.
点评:排列组合问题在几何图形中的应用,在计算时要求做到兼顾所有的条件,先排约束条件多的元素,做的不重不漏,注意实际问题本身的限制条件.

练习册系列答案
相关题目
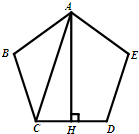 如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得
如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得 如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得
如图,正五边形ABCDE的边长为2,甲同学在△ABC中用余弦定理解得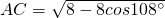 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得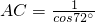 ,据此可得cos72°的值所在区间为
,据此可得cos72°的值所在区间为 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )
 ,乙同学在Rt△ACH中解得
,乙同学在Rt△ACH中解得 ,据此可得cos72°的值所在区间为( )
,据此可得cos72°的值所在区间为( )