题目内容
在数列{an}中,a1=1,an+an+1=3n.设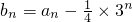
(1)求证:数列{bn}是等比数列
(2)求数列{an}的前n项的和
(3)设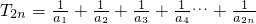 ,求证:T2n<3.
,求证:T2n<3.
证明:(1)由a1=1,an+an+1=3n,
得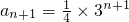 =
= ,
,
即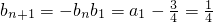 .
.
∴数列{bn}是首项为 ,公比为-1的等比数列.
,公比为-1的等比数列.
解:(2)由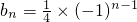 ,
,
得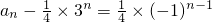 ,
,
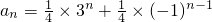 =
=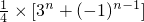
Sn=[3+32+33+…+3n+(-1)0+(-1)1+(-1)1+(-1)2+…+(-1)n-1]
=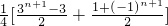 .
.
证明:(3)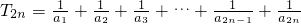
=
=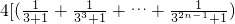 +
+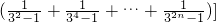
<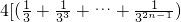 +
+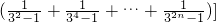
∵32n-1>32n-1,(n∈N*),
∴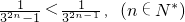 ,
,
∴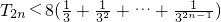
=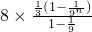
=3(1-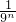 )<3.
)<3.
分析:(1)由a1=1,an+an+1=3n,得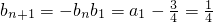 .由此能够证明数列{bn}是等比数列.
.由此能够证明数列{bn}是等比数列.
(2)由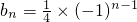 ,得
,得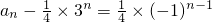 ,所以an=
,所以an=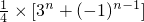 ,由此能求出数列{an}的前n项的和.
,由此能求出数列{an}的前n项的和.
(3)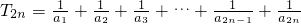 =
= =
=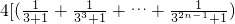 +
+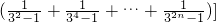 <
<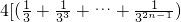 +
+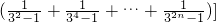 ,由此入手能够证明T2n<3.
,由此入手能够证明T2n<3.
点评:本题考查数列和不等式的综合应用,综合性强,难度大,易出错.解题时要认真审题,注意培养计算能力和转化能力.
得
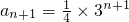 =
= ,
,即
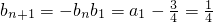 .
.∴数列{bn}是首项为
 ,公比为-1的等比数列.
,公比为-1的等比数列.解:(2)由
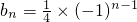 ,
,得
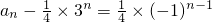 ,
,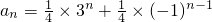 =
=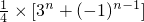
Sn=[3+32+33+…+3n+(-1)0+(-1)1+(-1)1+(-1)2+…+(-1)n-1]
=
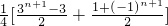 .
.证明:(3)
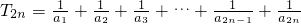
=

=
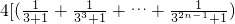 +
+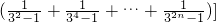
<
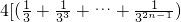 +
+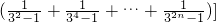
∵32n-1>32n-1,(n∈N*),
∴
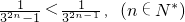 ,
,∴
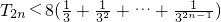
=
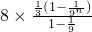
=3(1-
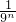 )<3.
)<3.分析:(1)由a1=1,an+an+1=3n,得
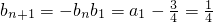 .由此能够证明数列{bn}是等比数列.
.由此能够证明数列{bn}是等比数列.(2)由
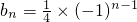 ,得
,得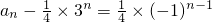 ,所以an=
,所以an=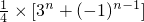 ,由此能求出数列{an}的前n项的和.
,由此能求出数列{an}的前n项的和.(3)
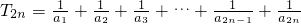 =
= =
=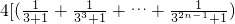 +
+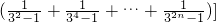 <
<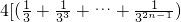 +
+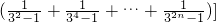 ,由此入手能够证明T2n<3.
,由此入手能够证明T2n<3.点评:本题考查数列和不等式的综合应用,综合性强,难度大,易出错.解题时要认真审题,注意培养计算能力和转化能力.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.