题目内容

3．空间直角坐标系中，点A坐标为（1，$\sqrt{3}$，2），且△MNP三个顶点分别满足：M是A在平面xOy上的射影点，N与A关于x轴对称，P与A关于平面xOz对称，则△MNP的面积为$4\sqrt{3}$．

分析 求出MNP的坐标，然后求解三角形的面积．

解答 解：空间直角坐标系中，点A坐标为（1，$\sqrt{3}$，2），且△MNP三个顶点分别满足：
M是A在平面xOy上的射影点（1，$\sqrt{3}$，0），
N与A关于x轴对称（1，-$\sqrt{3}$，-2），
P与A关于平面xOz对称（1，-$\sqrt{3}$，2），
则△MNP的面积为：$\frac{1}{2}×4×2\sqrt{3}$=$4\sqrt{3}$．
故答案为：$4\sqrt{3}$．

点评 本题考查空间向量的坐标运算，三角形的面积的求法，考查计算能力．

练习册系列答案
相关题目
14．在等差数列{an}中，若3（a4+a6）+2（a7+a9+a11）=24，则此数列的前13项之和为（　　）
A．13B．26C．52D．156
14．已知一组数据2，a，4，5的平均数为5，另一组数据为b，b+1，b+2，且a＜b，则新的一组数据2，a，4，5，b，b+1，b+2的中位数为9．
11．下列函数定义域是R且在区间（0，1）是递增函数的（　　）
A．y=|x+1|B．y=$\sqrt{x}$C．y=$\frac{1}{x}$D．y=-x2+4
18．函数y=$\sqrt{{x}^{2}-4x+13}$-$\sqrt{{x}^{2}+1}$的最大值是（　　）
A．2$\sqrt{2}$B．10C．$\sqrt{10}$D．0
8．已知函数f（x）=$\frac{x}{{x}^{2}+a}$（a＞0）在[1，+∞）上的最大值为$\frac{\sqrt{3}}{3}$，则a的值为（　　）
A．$\sqrt{3}$-1B．$\frac{3}{4}$C．$\frac{4}{3}$D．$\sqrt{3}$+1
15．下列说法正确的是（　　）
A．命题“若幂函数f（x）=xa在（0，+∞）内单调递减，则 a＜0”的逆否命题是“若a≥0，则幂函数f（x）=xa在（0，+∞）内单调递增”
B．已知命题p 和q，若p∧q为假命题，则命题p、q中必有一个是真命题、一个是假命题
C．若x，y∈R，则“x=y”是“$xy≥{（\frac{x+y}{2}）^2}$”的充要条件
D．若命题p：?x0∈R，x02+x0+1＜0，则￢p：?x∈R，x2+x+1＞0
11．已知数列{an}，若点（n，an）（n∈N+）均在直线y-3=k（x-6）上，则数列{an}的前11项和S11等于（　　）
A．18B．22C．33D．44
12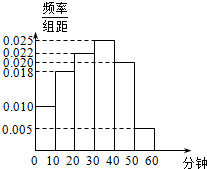．电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查．其中女性有55名．图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：
将日均收看该体育节目时间不低于40min的观众称为“体育迷”，已知“体育迷”中有10名女性．
（1）根据已知条件完成下面的2×2列表．
非体育迷体育迷总计
男
女
总计
（2）能否说在犯错误的概率不超过0.1的前提下，认为“体育迷”与性别有关？
P（K2≥k0）0.250.150.100.050.0250.0100.0050.001
k01.3232.0722.7063.8415.0246.6357.87910.828

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网