题目内容
22.已知函数(I)证明:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(II)对于给定的闭区间![]() ,试说明存在实数
,试说明存在实数 ![]() ,当
,当![]() 时,
时,![]() 在闭区间
在闭区间![]() 上是减函数;
上是减函数;
(III)证明:![]() .
.
(I)证明:由题设得g(x)=e2x-t(ex+1)+x,![]() (x)=2e2x-tex+1.
(x)=2e2x-tex+1.
又由2ex+e-x≥2![]() ,且t<2
,且t<2![]() 得t<2ex+e-x,即
得t<2ex+e-x,即
![]() (x)=2e2x-tex+1>0.
(x)=2e2x-tex+1>0.
由此可知,g(x)为R上的增函数.
(II)证法一:因为![]() (x)<0是g(x)为减函数的充分条件,所以只要找到实数k,使得t>k时,在闭区间[a,b]上成立即可.
(x)<0是g(x)为减函数的充分条件,所以只要找到实数k,使得t>k时,在闭区间[a,b]上成立即可.
因为y=2ex+e-x在闭区间[a,b]上连续,故在闭区间[a,b]上有最大值,设其为k,于是在t>k时,![]() (x)<0在闭区间[a,b]上恒成立,即g(x)在闭区间[a,b]上为减函数.
(x)<0在闭区间[a,b]上恒成立,即g(x)在闭区间[a,b]上为减函数.
证法二:因为![]() (x)<0是g(x)为减函数的充分条件,所以只要找到实数k,使得t>k时,
(x)<0是g(x)为减函数的充分条件,所以只要找到实数k,使得t>k时,
![]() (x)=2e2x-tex+1<0,
(x)=2e2x-tex+1<0,
在闭区间[a,b]上成立即可.
令m=ex,则![]() (x)<0(x∈[a,b])当且仅当
(x)<0(x∈[a,b])当且仅当
2m2-tm+1<0(m∈[ea,eb]).
而上式成立只需要

成立.取2ea+e-a与2eb+e-b中较大者记为k,易知当t>k, ![]() (x)<0在闭区间[a,b]上恒成立,即g(x)在闭区间[a,b]上为减函数.
(x)<0在闭区间[a,b]上恒成立,即g(x)在闭区间[a,b]上为减函数.
(III)证法一:设F(t)=2t2-2(ex+x)t+e2x+x2+1,即
F(t)=2![]()
易得
F(t)≥![]() (ex-x)2+1.
(ex-x)2+1.
令H(x)=ex-x,则![]() (x)=ex-1,易知
(x)=ex-1,易知![]() (0)=0.当x>0时.
(0)=0.当x>0时.![]() (x)>0;当x<0时,
(x)>0;当x<0时,![]() (x)<0.故当x=0时,H(x)取最小值,H(0)=1.所以
(x)<0.故当x=0时,H(x)取最小值,H(0)=1.所以
![]()
于是对任意x、t,有F(t)≥![]() ,即f(x) ≥
,即f(x) ≥![]() .
.
证法二:设F(t)=2t2-2(ex+x)t+e2x+x2+1,
F(x)≥![]() 当且仅当
当且仅当
2t2-2(ex+x)t+e2x+x2-![]() ≥0.
≥0.
只需证明
4(ex+x)2-2×4(e2x-x2-![]() )≤0,
)≤0,
即
(ex-x)2≥1.
以下同证法一
证法三:设F(t)=2t2-2(ex+x)t+e2x+x2+1,则
F′(t)=4t-2(ex+x).
易得F′(![]() )=0。当t>
)=0。当t>![]() 时,F′(t)>0;当t<
时,F′(t)>0;当t<![]() 时,F′(t)<0,故当t=
时,F′(t)<0,故当t=![]() 时,F(t)取最小值
时,F(t)取最小值![]()
F(t)≥![]() ( ex-x)2+1.
( ex-x)2+1.
以下同证法一.
证法四:f(x)=(ex-t)2+(x-t)2+1.
设点A、B的坐标分别为(x,ex)、(t,t),易知点B在直线y=x上,令点A到直线y=x的距离为d,则
f(x)=|AB|2+1≥d2+1=![]() (ex-x)2+1.
(ex-x)2+1.
以下同证法一.

 .
. 在
在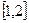 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; ,是否存在实数
,是否存在实数 时,函数
时,函数 的最小值是
的最小值是 ,若存在,求出实数
,若存在,求出实数 .
. .
. ;
; 的解集.
的解集.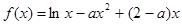 .
. 的单调性;
的单调性;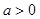 ,证明:当
,证明:当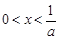 时,
时,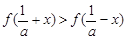 ;
;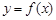 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明: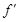 (x0)<0.
(x0)<0.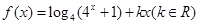 是偶函数.
是偶函数.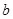 ,函数
,函数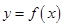 的图象与直线
的图象与直线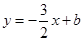 最多只有一个交点;
最多只有一个交点;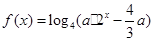 有且只有一个解,求实数
有且只有一个解,求实数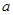 的取值范围.
的取值范围. .
. 在
在 上是减函数,求实数
上是减函数,求实数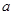 的取值范围;
的取值范围; ,是否存在实数
,是否存在实数 时,函数
时,函数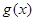 的最小值是
的最小值是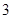 ,若存在,求出实数
,若存在,求出实数 .
.