Question

本小题满分12分）

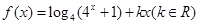已知函数是偶函数.

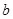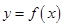(I)证明：对任意实数，函数的图象与直线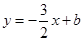最多只有一个交点；

(II)若方程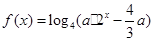有且只有一个解，求实数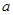的取值范围.

 

Answer 1

【答案】

（I）由函数是偶函数可得：

即对一切恒成立，

……………………………3分

由题意可知，只要证明函数在定义域上为单调函数即可.

任取且，则…………5分

，即，

……………6分

函数在上为单调增函数.

对任意实数，函数的图象与直线最多只有一个交点.………7分

（II）若方程有且只有一解，

也就是方程有且只有一个实根，

令，问题转化为方程：有且只有一个正根.………8分

（1）   若，则，不合题意；…………9分

（2）   若时，由或，当时，不合题意；当时，；……………10分

（3）   若时，，若方程一个正根与一个负根时，则.

………11分

综上：实数的取值范围是.……………12分

 

【解析】略