题目内容
已知一系列函数有如下性质:
函数y=x+
在(0,1]上是减函数,在[1,+∞)上是增函数;
函数y=x+
在(0,
]上是减函数,在[
,+∞)上是增函数;
函数y=x+
在(0,
]上是减函数,在[
,+∞)上是增函数;…
利用上述所提供的信息解决问题:若函数y=x+
(x>0)的值域是[6,+∞),则实数m的值是______.
函数y=x+
| 1 |
| x |
函数y=x+
| 2 |
| x |
| 2 |
| 2 |
函数y=x+
| 3 |
| x |
| 3 |
| 3 |
利用上述所提供的信息解决问题:若函数y=x+
| 3m |
| x |
∵函数y=x+
在(0,1]上是减函数,在[1,+∞)上是增函数;
函数y=x+
在(0,
]上是减函数,在[
,+∞)上是增函数;
函数y=x+
在(0,
]上是减函数,在[
,+∞)上是增函数;
∴函数y=x+
(p为正常数)在(0,
]上是减函数,在[
,+∞)上是增函数;
∵函数y=x+
(x>0)的值域是[6,+∞),
∴函数在x=
取得最小值为6,
∴
+
=6,
解得m=2,故答案为2.
| 1 |
| x |
函数y=x+
| 2 |
| x |
| 2 |
| 2 |
函数y=x+
| 3 |
| x |
| 3 |
| 3 |
∴函数y=x+
| p |
| x |
| p |
| p |
∵函数y=x+
| 3m |
| x |
∴函数在x=
| 3m |
∴
| 3m |
| 3m | ||
|
解得m=2,故答案为2.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
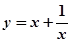 在
在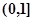 上是减函数,在
上是减函数,在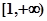 上是增函数;
上是增函数;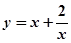 在
在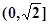 上是减函数,在
上是减函数,在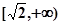 上是增函数;
上是增函数;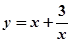 在
在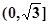 上是减函数,在
上是减函数,在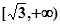 上是增函数;
上是增函数;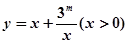 的值域是
的值域是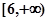 ,则实数
,则实数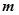 的值是 .
的值是 . 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 
 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 的值域是
的值域是 ,则实数
,则实数 的值是___________.
的值是___________. 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 
 在
在 上是减函数,在
上是减函数,在 上是增函数;………………
上是增函数;……………… 的值域是
的值域是 ,则实数
,则实数 是
是 在(0,1]上是减函数,在[1,+∞)上是增函数;
在(0,1]上是减函数,在[1,+∞)上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数;…
上是增函数;… 的值域是[6,+∞),则实数m的值是 .
的值域是[6,+∞),则实数m的值是 .