题目内容
已知一系列函数有如下性质:函数
 在(0,1]上是减函数,在[1,+∞)上是增函数;
在(0,1]上是减函数,在[1,+∞)上是增函数;函数
 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;函数
 在
在 上是减函数,在
上是减函数,在 上是增函数;…
上是增函数;…利用上述所提供的信息解决问题:若函数
 的值域是[6,+∞),则实数m的值是 .
的值域是[6,+∞),则实数m的值是 .
【答案】分析:根据一系列函数的性质进行归纳和类比,总结出函数y=x+ (p为常数)的性质和增减区间,从而求解.
(p为常数)的性质和增减区间,从而求解.
解答:解:∵函数 在(0,1]上是减函数,在[1,+∞)上是增函数;
在(0,1]上是减函数,在[1,+∞)上是增函数;
函数 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
函数 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
∴函数y=x+ (p为正常数)在(0,
(p为正常数)在(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数;
,+∞)上是增函数;
∵函数 的值域是[6,+∞),
的值域是[6,+∞),
∴函数在x= 取得最小值为6,
取得最小值为6,
∴ +
+ =6,
=6,
解得m=2,故答案为2.
点评:此题考查基本不等式的性质和学生的归纳与类比的能力,考查函数y=y=x+ 性质是高考经常出现的题型,在今后学习过程中要注意.
性质是高考经常出现的题型,在今后学习过程中要注意.
 (p为常数)的性质和增减区间,从而求解.
(p为常数)的性质和增减区间,从而求解.解答:解:∵函数
 在(0,1]上是减函数,在[1,+∞)上是增函数;
在(0,1]上是减函数,在[1,+∞)上是增函数;函数
 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;函数
 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;∴函数y=x+
 (p为正常数)在(0,
(p为正常数)在(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数;
,+∞)上是增函数;∵函数
 的值域是[6,+∞),
的值域是[6,+∞),∴函数在x=
 取得最小值为6,
取得最小值为6,∴
 +
+ =6,
=6,解得m=2,故答案为2.
点评:此题考查基本不等式的性质和学生的归纳与类比的能力,考查函数y=y=x+
 性质是高考经常出现的题型,在今后学习过程中要注意.
性质是高考经常出现的题型,在今后学习过程中要注意. 
练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
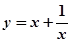 在
在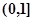 上是减函数,在
上是减函数,在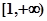 上是增函数;
上是增函数;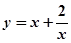 在
在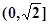 上是减函数,在
上是减函数,在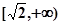 上是增函数;
上是增函数;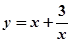 在
在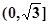 上是减函数,在
上是减函数,在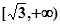 上是增函数;
上是增函数;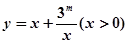 的值域是
的值域是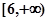 ,则实数
,则实数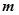 的值是 .
的值是 . 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 
 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 的值域是
的值域是 ,则实数
,则实数 的值是___________.
的值是___________. 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 
 在
在 上是减函数,在
上是减函数,在 上是增函数;………………
上是增函数;……………… 的值域是
的值域是 ,则实数
,则实数 是
是