题目内容
设函数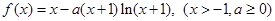 .
.
(1)求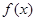 的单调区间;
的单调区间;
(2)当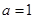 时,若方程
时,若方程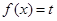 在
在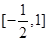 上有两个实数解,求实数
上有两个实数解,求实数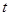 的取值范围;
的取值范围;
(3)证明:当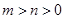 时,
时,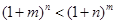 .
.
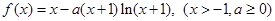 .
.(1)求
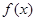 的单调区间;
的单调区间;(2)当
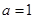 时,若方程
时,若方程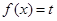 在
在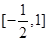 上有两个实数解,求实数
上有两个实数解,求实数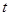 的取值范围;
的取值范围;(3)证明:当
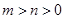 时,
时,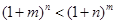 .
.(1)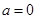 时,在
时,在 上是增函数;
上是增函数;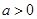 时,在
时,在 上单调递增,在
上单调递增,在 上单调递减.(2)
上单调递减.(2)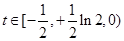 ,(3)详见解析
,(3)详见解析
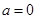 时,在
时,在 上是增函数;
上是增函数;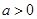 时,在
时,在 上单调递增,在
上单调递增,在 上单调递减.(2)
上单调递减.(2)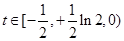 ,(3)详见解析
,(3)详见解析试题分析:(1)求函数单调区间,首先明确定义域,再求导
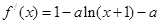 ,由于含有参数,需分类讨论根的情况.
,由于含有参数,需分类讨论根的情况. 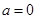 时,
时,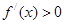 ,所以
,所以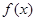 在
在 上是增函数.当
上是增函数.当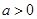 时,由
时,由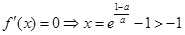 ,所以
,所以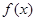 在
在 上单调递增,在
上单调递增,在 上单调递减.(2)本题考查函数与方程思想,实际研究直线
上单调递减.(2)本题考查函数与方程思想,实际研究直线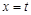 与函数
与函数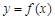 图像交点有两个的情况,由(1)知
图像交点有两个的情况,由(1)知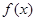 在
在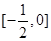 上单调递增,在
上单调递增,在 上单调递减,且
上单调递减,且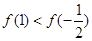 ,所以当
,所以当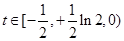 时,方程
时,方程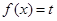 有两解.(3)本题关键在于构造函数,首先将两变量分离,这要用到取对数,即
有两解.(3)本题关键在于构造函数,首先将两变量分离,这要用到取对数,即 因此只需证
因此只需证 ,即证
,即证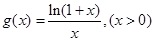 为单调减函数,可利用导数
为单调减函数,可利用导数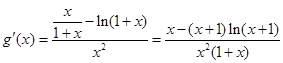 ,再结合(1)的结论,可证.
,再结合(1)的结论,可证.试题解析:(1)
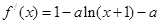 .
.①
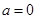 时,
时,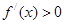 ,∴
,∴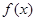 在
在 上是增函数. 1分
上是增函数. 1分②当
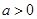 时,由
时,由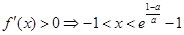 ,由
,由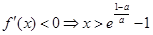 ,
,∴
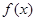 在
在 上单调递增,在
上单调递增,在 上单调递减. 4分
上单调递减. 4分(2)当
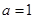 时,由(1)知,
时,由(1)知,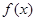 在
在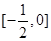 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,又
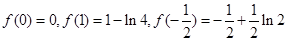 , 6分
, 6分∴
 .
.∴当
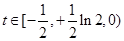 时,方程
时,方程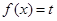 有两解. 8分
有两解. 8分(3)∵
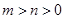 .∴要证:
.∴要证: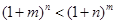 只需证
只需证
只需证:
 .
.设
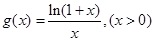 , 10分
, 10分则
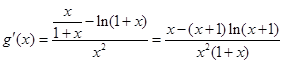 .
.由(1)知
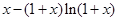 在
在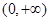 单调递减, 12分
单调递减, 12分∴
 ,即
,即 是减函数,而
是减函数,而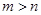 .
.∴
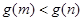 ,故原不等式成立. 14分
,故原不等式成立. 14分
练习册系列答案
相关题目
 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计) (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为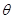 的函数
的函数 ;
;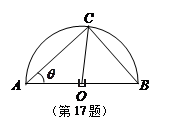
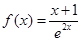 .
.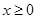 时,
时,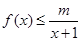 恒成立,求m的取值范围;
恒成立,求m的取值范围;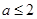 时,求证:
时,求证: .
.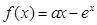
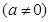 .
.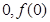 )处的切线方程;
)处的切线方程; 使得
使得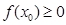 ,求
,求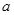 的取值范围.
的取值范围.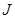 型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,
型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算, (单位:
(单位: )与速度
)与速度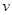 (单位:km/h)的关系近似地满足
(单位:km/h)的关系近似地满足 ,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.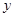 (元)(不计返程费用),将
(元)(不计返程费用),将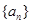 的前
的前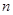 项和为
项和为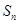 ,对一切正整数
,对一切正整数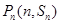 都在函数
都在函数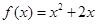 的图像上,且过点
的图像上,且过点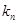 .
.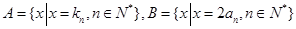 ,等差数列
,等差数列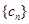 的任一项
的任一项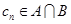 ,其中
,其中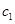 是
是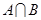 中所有元素的最小数,
中所有元素的最小数,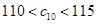 ,求
,求 在点
在点 处的切线与两坐标轴围成的三角形的面积为
处的切线与两坐标轴围成的三角形的面积为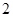 ,则实数
,则实数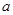 的值是_______.
的值是_______.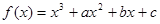 ,在定义域
,在定义域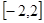 上表示的曲线过原点,且在
上表示的曲线过原点,且在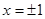 处的切线斜率均为
处的切线斜率均为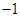 .有以下命题:
.有以下命题: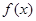 是奇函数;②若
是奇函数;②若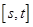 内递减,则
内递减,则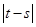 的最大值为4;③
的最大值为4;③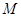 ,最小值为
,最小值为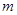 ,则
,则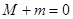 ; ④若对
; ④若对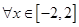 ,
,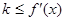 恒成立,则
恒成立,则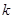 的最大值为2.其中正确命题的序号为
的最大值为2.其中正确命题的序号为  的图象与
的图象与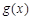 的图象关于直线
的图象关于直线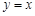 对称。
对称。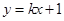 与
与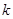 的值;
的值;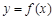 与曲线
与曲线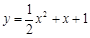 公共点的个数.
公共点的个数.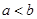 ,比较
,比较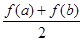 与
与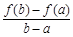 的大小, 并说明理由.
的大小, 并说明理由.