题目内容
(本题满分14分)
设函数 ,其中
,其中 .⑴若
.⑴若 的定义域为区间
的定义域为区间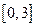 ,求
,求 的最
的最
大值和最小值;⑵若 的定义域为区间
的定义域为区间 ,求
,求 的取值范围,使
的取值范围,使 在定义域
在定义域
内是单调减函数。
设函数
 ,其中
,其中 .⑴若
.⑴若 的定义域为区间
的定义域为区间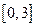 ,求
,求 的最
的最大值和最小值;⑵若
 的定义域为区间
的定义域为区间 ,求
,求 的取值范围,使
的取值范围,使 在定义域
在定义域内是单调减函数。
⑴
(2)当 时,
时, 在定义域
在定义域 内是单调减函数
内是单调减函数

(2)当
 时,
时, 在定义域
在定义域 内是单调减函数
内是单调减函数 ,
,设
 ,则
,则
⑴当
 时,设
时,设 ,则
,则 ,
,又

 在
在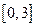 上是增函数,
上是增函数,
⑵设
 ,则
,则
要
 在
在 上是减函数,只要
上是减函数,只要 ,
, 而
 ,
,∴
 当
当 ,即
,即 时,有
时,有 ,
,
∴当
 时,
时, 在定义域
在定义域 内是单调减函数。
内是单调减函数。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
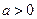 且
且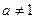 ,
,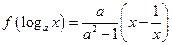
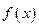 的表达式; (2)判断
的表达式; (2)判断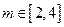 时,
时,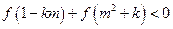 恒成立,求
恒成立,求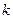 的取值范围.
的取值范围.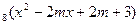 的定义域为R,则实数m的取值范围是
的定义域为R,则实数m的取值范围是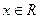 ,f(x+2)="--" f(x),当
,f(x+2)="--" f(x),当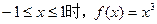 .
.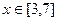 时,求f(x)的解析式。
时,求f(x)的解析式。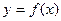 ,若同时满足下列条件:①
,若同时满足下列条件:①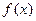 在D内单调
在D内单调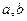 ]
]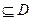 ,使
,使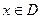 )叫闭函数。
)叫闭函数。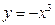 符合条件②的区间[
符合条件②的区间[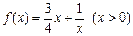 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;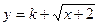 是闭函数,求实数
是闭函数,求实数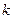 的取值范围。
的取值范围。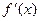 >0,
>0,  >0,则x<0时( )
>0,则x<0时( )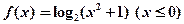 的反函数是_______ ___.
的反函数是_______ ___. 是定义在
是定义在 上的函数,
上的函数, ,且
,且 =5,
=5, =
=  .
. ,则
,则 ( )
( )