题目内容
如图所示,已知在△ABC边上做匀速运动的点D、E、F,在时刻t=0时,分别从A、B、C出发,各以一定速度向B、C、A前进,当时刻t=1时到达B、C、A.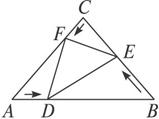
(1)问:在运动过程中,△DEF的重心发生怎样的变化?
(2)若△ABC的面积是S,则△DEF的面积有最小值吗?若有,则何时取到最小值?若无,请说明理由.
思路分析:(1)注意在同一时刻D、E、F分
、
、
所成的比相同,故可利用定比分点坐标公式分别求出D、E、F三点的坐标,再利用重心坐标公式求出重心坐标.
(2)将S△DEF表示为t的二次函数求最小值,注意t的范围.
解:(1)设A(xA,yA),B(xB,yB),C(xC,yC).
由题意,在同一时刻t,D、E、F分
、
、
所成的比相同,设为λ,则λ=
=
=
=
.
由定比分点坐标公式可求得
D(txB+(1-t)xA,tyB+(1-t)yA),
E(txC+(1-t)xB,tyC+(1-t)yB),
F(txA+(1-t)xC,tyA+(1-t)yC).
由三角形重心坐标公式求得
△DEF的重心坐标为
(
,
),与t无关,
即在运动过程中,△DEF的重心不变.
(2)∵
=t,
=1-t,
∴△DFA与△ABC的底与高对应成比例,S△DFA∶S△ABC=(AD·AF)∶(AB·AC)=t(1-t),即S△DFA=t(1-t)S.
同理,S△DEB=S△EFC=t(1-t)S.
∴S△DEF=S△ABC-(S△DFA+S△DEB+S△EFC)
=(3t2-3t+1)S=［3(t-
)2+
］S.
∵0≤t≤1,
∴当t=
时,S△DEF的面积有最小值为
S.
练习册系列答案
相关题目
，已知在矩形ABCD中，AB=1，BC=a（a＞0），PA⊥平面ABCD，且PA=1．
如图所示，已知在矩形ABCD中，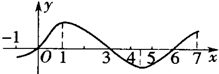
设定义在[-1，7]上的函数y=f（x）的图象如图所示．已知（a，b）是
