题目内容
设△ABC的内角A、B、C的对边长分别为a、b、c,cos(A-C)+cosB=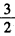 ,b2=ac,求B。
,b2=ac,求B。
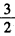 ,b2=ac,求B。
,b2=ac,求B。 解:由cos(A-C)+cosB=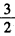 ,及B=π-(A+C),
,及B=π-(A+C),
得cos(A-C)-cos(A+C)=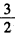 ,
,
cosAcosC+sinAsinC-(cosAcosC-sinAsinC)=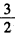 ,
,
sinAsinC=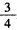 ,
,
又由b2=ac及正弦定理得sin2B=sinAsinC,
故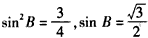 或
或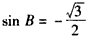 (舍去),
(舍去),
于是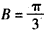 或
或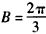 ,
,
又由b2=ac知b≤a或b≤c,所以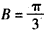 。
。
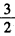 ,及B=π-(A+C),
,及B=π-(A+C),得cos(A-C)-cos(A+C)=
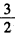 ,
,cosAcosC+sinAsinC-(cosAcosC-sinAsinC)=
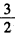 ,
,sinAsinC=
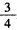 ,
,又由b2=ac及正弦定理得sin2B=sinAsinC,
故
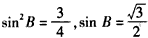 或
或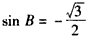 (舍去),
(舍去),于是
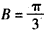 或
或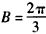 ,
,又由b2=ac知b≤a或b≤c,所以
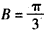 。
。 
练习册系列答案
相关题目