题目内容
设函数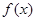 对任意
对任意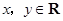 ,都有
,都有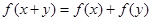 且
且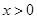 时,
时,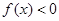 .
.
(Ⅰ)证明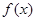 为奇函数;
为奇函数;
(Ⅱ)证明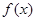 在
在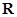 上为减函数.
上为减函数.
【答案】
见解析。
【解析】
试题分析:
证明:(Ⅰ) ,且
,且 .
.
 令
令 ,
, ,
,
 .令
.令 代入
代入 .
.
得 (
( ).
).
 是奇函数.
是奇函数.
(Ⅱ)任取 ,且
,且 ,
,
则 .
.
 .
.
又 ,
,
 为奇函数,
为奇函数, .
.
 .
.
即 .
.
 在
在 上是减函数.
上是减函数.
考点:本题主要考查函数的性质、综合法的定义和方法。
点评:赋值法常常应用于抽象函数的讨论。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 对任意实数
对任意实数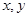 都有
都有 且
且 时
时 。
。  内是增函数;
内是增函数; ,试求
,试求 的取值范围。
的取值范围。 对任意实数
对任意实数 都有
都有 且
且 时
时 。
。 内是增函数;
内是增函数; ,试求
,试求 的取值范围。
的取值范围。 对任意实数
对任意实数 都有
都有 且
且 时
时 。
。  内是增函数;
内是增函数; ,试求
,试求 的取值范围。
的取值范围。