题目内容
(理)某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
由于部分数据技失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为
.
(1)试确定a、b的值;
(2)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(3)从视觉记忆能力偏高的学生中任意抽取3人,设具有听觉记忆能力中等的学生人数为ξ,求随机变量ξ的数学期望Eξ.
| 视觉 听觉 | 视觉记忆能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 | b | |
| 偏高 | 2 | a | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
| 2 |
| 5 |
(1)试确定a、b的值;
(2)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(3)从视觉记忆能力偏高的学生中任意抽取3人,设具有听觉记忆能力中等的学生人数为ξ,求随机变量ξ的数学期望Eξ.
考点:离散型随机变量的期望与方差,列举法计算基本事件数及事件发生的概率,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)由表格数据知,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的学生共有(10+a)人,记“视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上”为事件A,由P(A)=
=
,能确定a、b的值.
(Ⅱ)由表格数据知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人,由此利用对立事件概率计算公式能求出至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率.
(Ⅲ)具有视觉记忆能力偏高的学生共有9人,其中听觉记忆能力中等的学生有3位,则9位学生中任意抽取3位,ξ的可能取值为0,1,2,3,由此能求出随机变量ξ的数学期望Eξ.
| 10+a |
| 40 |
| 2 |
| 5 |
(Ⅱ)由表格数据知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人,由此利用对立事件概率计算公式能求出至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率.
(Ⅲ)具有视觉记忆能力偏高的学生共有9人,其中听觉记忆能力中等的学生有3位,则9位学生中任意抽取3位,ξ的可能取值为0,1,2,3,由此能求出随机变量ξ的数学期望Eξ.
解答:
解:(Ⅰ)由表格数据知,视觉记忆能力恰为中等,
且听觉记忆能力为中等或中等以上的学生共有(10+a)人,
记“视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上”为事件A,
则P(A)=
=
,解得a=6,
∴b=40-(32+a)=40-38=2.
(Ⅱ)由表格数据知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人,
记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件B,
则“没有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件
,
∴P(B)=1-P(
)=1-
=1-
=
.
∴从40人中任意抽取3人,
其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率为
.
(Ⅲ)具有视觉记忆能力偏高的学生共有9人,其中听觉记忆能力中等的学生有3位,
则9位学生中任意抽取3位,ξ的可能取值为0,1,2,3,
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,
∴Eξ=0×
+1×
+2×
+3×
=1.
且听觉记忆能力为中等或中等以上的学生共有(10+a)人,
记“视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上”为事件A,
则P(A)=
| 10+a |
| 40 |
| 2 |
| 5 |
∴b=40-(32+a)=40-38=2.
(Ⅱ)由表格数据知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人,
记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件B,
则“没有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件
. |
| B |
∴P(B)=1-P(
. |
| B |
| ||
|
| 124 |
| 247 |
| 123 |
| 247 |
∴从40人中任意抽取3人,
其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率为
| 123 |
| 247 |
(Ⅲ)具有视觉记忆能力偏高的学生共有9人,其中听觉记忆能力中等的学生有3位,
则9位学生中任意抽取3位,ξ的可能取值为0,1,2,3,
P(ξ=0)=
| ||
|
| 5 |
| 21 |
P(ξ=1)=
| ||||
|
| 15 |
| 28 |
P(ξ=2)=
| ||||
|
| 3 |
| 14 |
P(ξ=3)=
| ||
|
| 1 |
| 84 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 5 |
| 21 |
| 15 |
| 28 |
| 3 |
| 14 |
| 1 |
| 84 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
相关题目
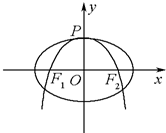 如图,抛物线C:y=-
如图,抛物线C:y=-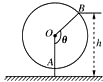 如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h.
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h. 已知a、b、c为集合A={1,2,3,4,5}中三个不同的数,如框图给出的一个算法运行后输出一个整数a,则输出的数a=4的概率是
已知a、b、c为集合A={1,2,3,4,5}中三个不同的数,如框图给出的一个算法运行后输出一个整数a,则输出的数a=4的概率是