题目内容
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了五次实验,得到的数据列表如下:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了五次实验,得到的数据列表如下:| 零件的数量x(个) | 2 | 3 | 4 | 5 | 6 |
| 所需时间y(小时) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(Ⅱ)求出y关于x的线性同归方程
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
考点:线性回归方程
专题:概率与统计
分析:(Ⅰ)在如图给定的坐标系中划出表中数据的散点图;
(Ⅱ)求出
,
,以及
,利用
=
-
求出
,即可y关于x的线性同归方程
=
x+
,并在(Ⅰ)的坐标系中画出同归直线(
(Ⅱ)求出
. |
| x |
. |
| y |
| ? |
| b |
 |
| a |
. |
| y |
 |
| b |
. |
| x |
| ? |
| a |
 |
| y |
 |
| b |
 |
| a |
解答:
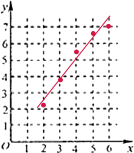 解:(Ⅰ)在如图给定的坐标系中划出表中数据的散点图,如图:
解:(Ⅰ)在如图给定的坐标系中划出表中数据的散点图,如图:
(Ⅱ)由题意可知
=
=4,
=
=5,
xi2=90,
xiyi=112.3,
=
=
=1.23,
=
-
=5-1.23×4=0.08,
回归直线方程为:
=1.23x+0.08,在(Ⅰ)的坐标系中画出同归直线如图.
 解:(Ⅰ)在如图给定的坐标系中划出表中数据的散点图,如图:
解:(Ⅰ)在如图给定的坐标系中划出表中数据的散点图,如图:(Ⅱ)由题意可知
. |
| x |
| 2+3+4+5+6 |
| 5 |
. |
| y |
| 2.2+3.8+5.5+6.5+7 |
| 5 |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
 |
| b |
| |||||||
|
| 112.3-5×4×5 |
| 90-5×42 |
 |
| a |
. |
| y |
 |
| b |
. |
| x |
回归直线方程为:
| ? |
| y |
点评:本题考查回归直线方程的应用,散点图的画法,基本知识的考查.

练习册系列答案
相关题目
 如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为
如图,四边形ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF,BE与平面ABCD所成角的正切值为 E为圆内两弦AB和CD的交点,过点E作AD的平行线交BC的延长线于点F.
E为圆内两弦AB和CD的交点,过点E作AD的平行线交BC的延长线于点F.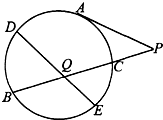 如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3
如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3