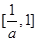题目内容
设函数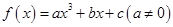 为奇函数,其图象在点
为奇函数,其图象在点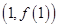 处的切线与直线
处的切线与直线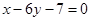 垂直,导函数
垂直,导函数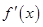 的最小值为
的最小值为 .
.
(1)求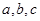 的值;
的值;
(2)求函数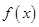 的单调递增区间,并求函数
的单调递增区间,并求函数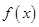 在
在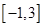 上的最大值和最小值.
上的最大值和最小值.
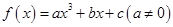 为奇函数,其图象在点
为奇函数,其图象在点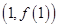 处的切线与直线
处的切线与直线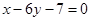 垂直,导函数
垂直,导函数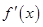 的最小值为
的最小值为 .
.(1)求
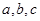 的值;
的值;(2)求函数
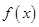 的单调递增区间,并求函数
的单调递增区间,并求函数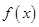 在
在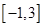 上的最大值和最小值.
上的最大值和最小值.(1) (2) 最大值是
(2) 最大值是 ,最小值是
,最小值是 .
.
 (2) 最大值是
(2) 最大值是 ,最小值是
,最小值是 .
.试题分析:(1)利用函数为奇函数,建立恒等式
 ?①,切线与已知直线垂直得
?①,切线与已知直线垂直得 ?②导函数的最小值得
?②导函数的最小值得 ?③.解得
?③.解得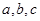 的值;
的值;(2)通过导函数求单调区间及最大值,最小值.
试题解析:(1)因为
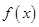 为奇函数,
为奇函数,所以
 即
即 ,所以
,所以 , 2分
, 2分因为
 的最小值为
的最小值为 ,所以
,所以 , 4分
, 4分又直线
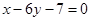 的斜率为
的斜率为 ,
,因此,
 ,
,∴
 . 6分
. 6分(2)单调递增区间是
 和
和 . 9分
. 9分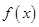 在
在 上的最大值是
上的最大值是 ,最小值是
,最小值是 . 12分
. 12分
练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;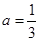 时,求函数
时,求函数 ,若对于
,若对于 [1,2],
[1,2], [0,1],使
[0,1],使 成立,求实数
成立,求实数 的取值范围.
的取值范围.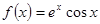 的图像在点
的图像在点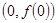 处的切线的倾斜角为( )
处的切线的倾斜角为( )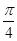
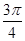
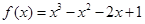 相切的直线有 条(以数字作答).
相切的直线有 条(以数字作答). 在
在 处的切线平行于直线
处的切线平行于直线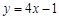 ,则
,则 分别是自然对数的底和圆周率,则下列不等式不成立的是( )
分别是自然对数的底和圆周率,则下列不等式不成立的是( )



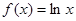 ,且
,且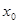 ,
,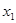 ,
,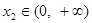 ,下列命题:
,下列命题: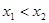 ,则
,则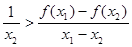
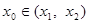 ,
,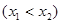 ,使得
,使得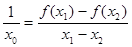
 ,
,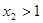 ,则
,则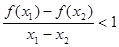
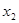 ,都有
,都有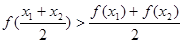
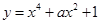 在点
在点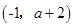 处切线的斜率为8,
处切线的斜率为8,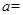 ( )
( )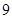
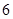
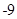
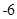
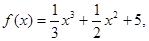 则函数
则函数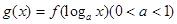 的单调递增区间是( )
的单调递增区间是( )