Question

【题目】已知函数.

（Ⅰ）求函数的单调区间;

（Ⅱ）若, ,求函数图像上任意一点处切线斜率的取值范围.

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ） .

【解析】试题分析：本题主要考查导数的运算、导数的几何意义、利用导数判断函数的单调性、利用导数求函数的最值、利用导数求函数的切线方程等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力．第一问，先求函数的定义域，对求导，对和进行讨论，利用和判断函数的单调性；第二问，对求导，根据导数的几何意义，需要k的取值范围，需求的最值，对再求导，判断单调性，得到函数的最大和最小值．

试题解析：（Ⅰ）函数的定义域为．

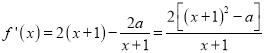
当时， 在上恒成立，于是在定义域内单调递增．

当时， 得

当变化时， 变化情况如下

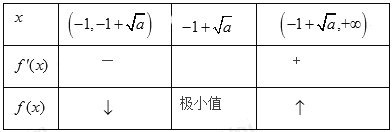
所以的单调递增区间是，单调递减区间是．

综上，当时， 单调递增区间是，

当时， 的单调递增区间是，单调递减区间是．

（Ⅱ）当时， ，令， 则，故为区间上增函数，所以，根据导数的几何意义可知．