题目内容
如图1,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连接EF,A'B(如图2).
(1)求证:A'D⊥EF;
(2)求点A'到平面BEDF的距离.
【答案】分析:(1)根据折叠前AD⊥AE,CD⊥CF,可得折叠后A'D⊥A'E,A'D⊥A'F,再由纡面垂直的判定定理可得A'D⊥平面A'EF,再由线面垂直的性质可得A'D⊥EF;
(2)利用割补法求出四边形BEDF的面积,及三角形BEF和三角形DEF的面积,求出三棱锥A'DEF的体积后,利用等积法,可求出点A'到平面BEDF的距离.
解答:解:(1)在正方形ABCD中,有AD⊥AE,CD⊥CF…(1分)
则A'D⊥A'E,A'D⊥A'F…(2分)
又A'E∩A'F=A',A'E,A'F?平面A'EF…(3分)
∴A'D⊥平面A'EF…(4分)
而EF?平面A'EF,
∴A'D⊥EF…(5分)
(2)∵正方形ABCD的边长为2,点E是AB的中点,点F是BC的中点
∴ …(6分)
…(6分)
∵ …(7分)
…(7分)
∴ …(8分)
…(8分)
在Rt△BEF中,BE=BF=1,∴
而A'E=A'F=1,
∴A'E2+A'F2=EF2…(9分)
∴ …(10分)
…(10分)
由(1)得A'D⊥平面A'EF,且A'D=2,
∴ …(11分)
…(11分)
设点A'到平面BEDF的距离为h,则 …(12分)
…(12分)
∴ …(13分)
…(13分)
∴点A'到平面BEDF的距离为 …(14分)
…(14分)
点评:本题考查的知识点是直线与平面垂直的性质,点到平面的距离,其中(1)的关键是弄清折叠前后不变的线线垂直关系,(2)的关键是求出三棱锥A'DEF的体积
(2)利用割补法求出四边形BEDF的面积,及三角形BEF和三角形DEF的面积,求出三棱锥A'DEF的体积后,利用等积法,可求出点A'到平面BEDF的距离.
解答:解:(1)在正方形ABCD中,有AD⊥AE,CD⊥CF…(1分)
则A'D⊥A'E,A'D⊥A'F…(2分)
又A'E∩A'F=A',A'E,A'F?平面A'EF…(3分)
∴A'D⊥平面A'EF…(4分)
而EF?平面A'EF,
∴A'D⊥EF…(5分)
(2)∵正方形ABCD的边长为2,点E是AB的中点,点F是BC的中点
∴
 …(6分)
…(6分)∵
 …(7分)
…(7分)∴
 …(8分)
…(8分)在Rt△BEF中,BE=BF=1,∴

而A'E=A'F=1,
∴A'E2+A'F2=EF2…(9分)
∴
 …(10分)
…(10分)由(1)得A'D⊥平面A'EF,且A'D=2,
∴
 …(11分)
…(11分)设点A'到平面BEDF的距离为h,则
 …(12分)
…(12分)∴
 …(13分)
…(13分)∴点A'到平面BEDF的距离为
 …(14分)
…(14分)点评:本题考查的知识点是直线与平面垂直的性质,点到平面的距离,其中(1)的关键是弄清折叠前后不变的线线垂直关系,(2)的关键是求出三棱锥A'DEF的体积

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
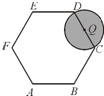 如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量
如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量| AP |
| AB |
| AF |
| A、(1,2] |
| B、[5,6] |
| C、[2,5] |
| D、[3,5] |
 (2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量
(2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量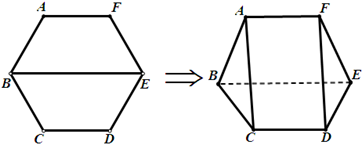 (2012•江西模拟)如图,把边长为2的正六边形ABCDEF沿对角线BE折起,使
(2012•江西模拟)如图,把边长为2的正六边形ABCDEF沿对角线BE折起,使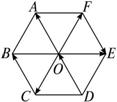
 如图,把边长为2的正六边形ABCDEF沿对角线BE折起,使
如图,把边长为2的正六边形ABCDEF沿对角线BE折起,使 .
.