题目内容
已知数列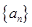 满足递推式:
满足递推式: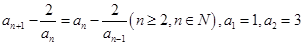 .
.
(Ⅰ)若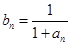 ,求
,求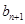 与
与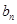 的递推关系(用
的递推关系(用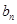 表示
表示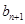 );
);
(Ⅱ)求证: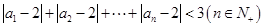 .
.
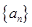 满足递推式:
满足递推式: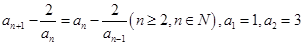 .
.(Ⅰ)若
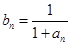 ,求
,求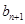 与
与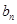 的递推关系(用
的递推关系(用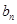 表示
表示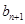 );
);(Ⅱ)求证:
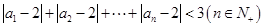 .
.(Ⅰ)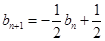 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
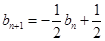 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)要得
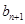 与
与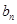 的递推关系,首先找到
的递推关系,首先找到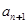 与
与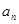 的递推关系.由
的递推关系.由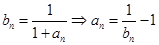 ,
,代入
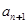 与
与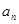 的递推关系便可得
的递推关系便可得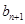 与
与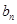 的递推关系.
的递推关系.(Ⅱ)由(Ⅰ)可得:

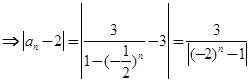
数列中涉及前
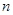 项和的不等式的证明,一般有两个大的方向,一种是先求和,后放缩;一种是先放缩,后求和.在本题中显然不可能先求和.所以选择先放缩后求和的方法.本题中
项和的不等式的证明,一般有两个大的方向,一种是先求和,后放缩;一种是先放缩,后求和.在本题中显然不可能先求和.所以选择先放缩后求和的方法.本题中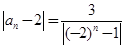 还是一个有绝对值符号的式子,所以还应去掉绝对值符号.在去绝对值符号时,需要对
还是一个有绝对值符号的式子,所以还应去掉绝对值符号.在去绝对值符号时,需要对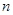 分奇数与偶数讨论:
分奇数与偶数讨论: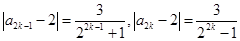 ,注意这里的分母,一个是加1,一个是减1,这种情况下,不能单独放缩,而是将两项相加后再放缩.
,注意这里的分母,一个是加1,一个是减1,这种情况下,不能单独放缩,而是将两项相加后再放缩.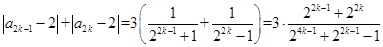
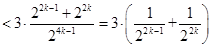 ,这样再分
,这样再分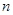 是奇数和偶数,就可使问题得证.
是奇数和偶数,就可使问题得证.试题解析:(Ⅰ)

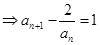 …………………①
…………………①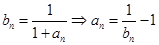 代入①式得
代入①式得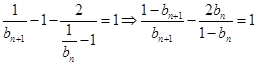 ,
,即
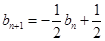 .
.(Ⅱ)
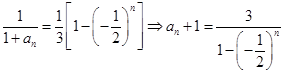
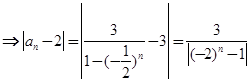 .
.对
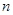 分奇数与偶数讨论:
分奇数与偶数讨论: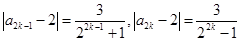 ,则
,则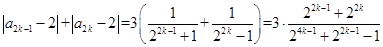
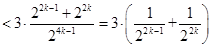 ,则
,则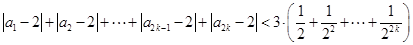
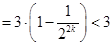 ;
;又
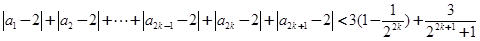
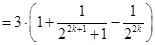
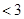 .
.综上所述,原不等式成立.

练习册系列答案
相关题目
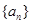 的前
的前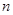 项和为
项和为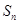 ,若
,若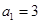 ,点
,点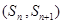 在直线
在直线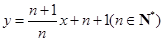 上.
上.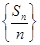 是等差数列;
是等差数列;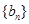 满足
满足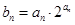 ,求数列
,求数列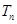 ;
;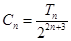 ,求证:
,求证: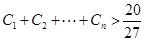 .
.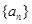 为公差不为
为公差不为 的等差数列,
的等差数列,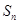 为前
为前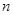 项和,
项和,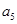 和
和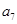 的等差中项为
的等差中项为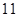 ,且
,且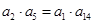 .令
.令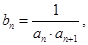 数列
数列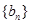 的前
的前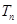 .
.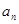 及
及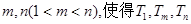 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的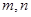 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.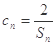 ,数列{cn}的前n项和为Tn,求证
,数列{cn}的前n项和为Tn,求证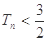
 的公差
的公差 ,前
,前 项和
项和 满足:
满足: ,那么数列
,那么数列 中最大的值是( )
中最大的值是( )



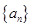 为等比数列,且
为等比数列,且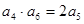 ,设等差数列
,设等差数列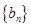 的前n项和为
的前n项和为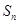 ,若
,若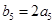 ,则
,则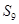 =( )
=( )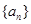 满足
满足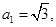
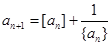
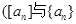 分别表示
分别表示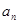 的整数部分与分数部分),则
的整数部分与分数部分),则 .
.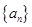 中,若
中,若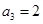 ,则
,则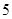 项和
项和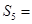 ( )
( )
 的首项
的首项 ,若
,若 ,
, ,则
,则 .
.