题目内容
6.一个几何体的三视图如图所示,则这个几何体的体积为( )
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{6}$ |
分析 由已知中的三视图可得:该几何体是两个以俯视图为底面的四棱锥组成的组合体,进而得到答案.
解答 解:由已知中的三视图可得:该几何体是两个以俯视图为底面的四棱锥组成的组合体,
底面底面面积为:1×1=1,
高均为:$\frac{\sqrt{2}}{2}$,
故体积V=2×$\frac{1}{3}$×1×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{3}$,
故选:C.
点评 本题考查的知识点是棱锥的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
16.执行如图所示的程序框图,正确的是( )
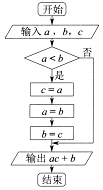

| A. | 若输入a,b,c的值依次为1,2,3,则输出的值为5 | |
| B. | 若输入a,b,c的值依次为1,2,3,则输出的值为7 | |
| C. | 若输入a,b,c的值依次为2,3,4,则输出的值为8 | |
| D. | 若输入a,b,c的值依次为2,3,4,则输出的值为10 |
17.设双曲线的虚轴长为2,焦距为$2\sqrt{3}$,则双曲线的渐近线方程为( )
| A. | $y=±\sqrt{2}x$ | B. | y=±2x | C. | $y=±\frac{{\sqrt{2}}}{2}x$或y=$±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
14.运行如图所示的程序框图,若输入的实数为2,则输出的n为( )
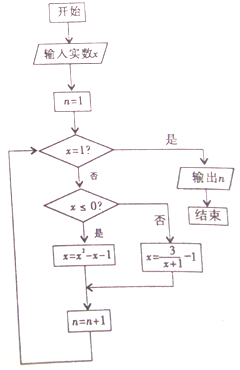

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )

| A. | 36 | B. | 48 | C. | 64 | D. | 72 |