题目内容
在数列{an}中,a1=1、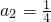 ,且
,且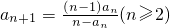 .
.
(Ⅰ) 求a3、a4,猜想an的表达式,并加以证明;
(Ⅱ) 设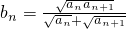 ,求证:对任意的自然数n∈N*,都有
,求证:对任意的自然数n∈N*,都有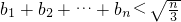 .
.
(Ⅰ) 解:(1)∵a1=1、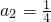 ,且
,且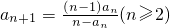 ,
,
∴a3=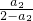 =
= ,
, =
=
故可以猜想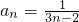 ,下面利用数学归纳法加以证明:
,下面利用数学归纳法加以证明:
(i) 显然当n=1,2,3,4时,结论成立,
(ii) 假设当n=k(k≥4),结论也成立,即
那么当n=k+1时,由题设与归纳假设可知: =
=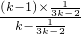 =
=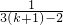
即当n=k+1时,结论也成立,
综上,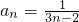 成立.
成立.
(Ⅱ)证明: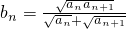 =
=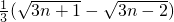
所以b1+b2+…+bn= =
=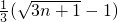
所以只需要证明
只需证明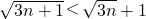
只需证明:3n+1<3n+2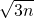 +1
+1
只需证明0<2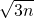 ,显然成立
,显然成立
所以对任意的自然数n∈N*,都有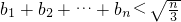 .
.
分析:(Ⅰ) 利用数列递推式,代入计算可得a3、a4,由此猜想an的表达式,再利用数学归纳法进行证明,证明n=k+1时,由题设与归纳假设,可得结论;
(Ⅱ)先对通项化简,再用裂项法求和,进而利用分析法进行证明即可.
点评:本题考查数列递推式,考查数列通项的猜想与证明,考查数列的求和与分析法证明的运用,属于中档题.
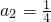 ,且
,且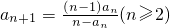 ,
,∴a3=
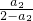 =
= ,
, =
=
故可以猜想
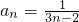 ,下面利用数学归纳法加以证明:
,下面利用数学归纳法加以证明:(i) 显然当n=1,2,3,4时,结论成立,
(ii) 假设当n=k(k≥4),结论也成立,即

那么当n=k+1时,由题设与归纳假设可知:
 =
=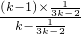 =
=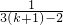
即当n=k+1时,结论也成立,
综上,
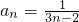 成立.
成立.(Ⅱ)证明:
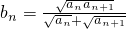 =
=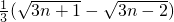
所以b1+b2+…+bn=
 =
=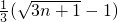
所以只需要证明

只需证明
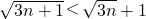
只需证明:3n+1<3n+2
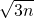 +1
+1只需证明0<2
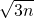 ,显然成立
,显然成立所以对任意的自然数n∈N*,都有
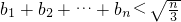 .
.分析:(Ⅰ) 利用数列递推式,代入计算可得a3、a4,由此猜想an的表达式,再利用数学归纳法进行证明,证明n=k+1时,由题设与归纳假设,可得结论;
(Ⅱ)先对通项化简,再用裂项法求和,进而利用分析法进行证明即可.
点评:本题考查数列递推式,考查数列通项的猜想与证明,考查数列的求和与分析法证明的运用,属于中档题.

练习册系列答案
相关题目
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.