题目内容
已知函数 与
与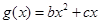 的图像都过点
的图像都过点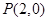 ,且它们在点
,且它们在点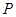 处有公共切线.
处有公共切线.
(1)求函数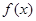 和
和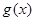 的表达式及在点
的表达式及在点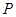 处的公切线方程;
处的公切线方程;
(2)设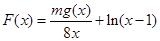 ,其中
,其中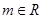 ,求
,求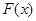 的单调区间.
的单调区间.
【答案】
(1)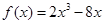 ,
,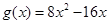 ,
,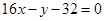 ;
;
(2)当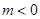 时,F(x)的单调减区间是
时,F(x)的单调减区间是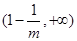 单调增区间是
单调增区间是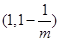 ;
;
当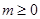 时,F(x)没有单调减区间,单调增区间是
时,F(x)没有单调减区间,单调增区间是 .
.
【解析】
试题分析:(1)因为函数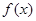 和
和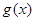 有公共的切线,所以切线的斜率相同,又因为它们都过
有公共的切线,所以切线的斜率相同,又因为它们都过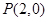 ,所以可以列出方程,求出
,所以可以列出方程,求出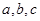 ;(2)先求导数,求出函数的定义域,通过讨论
;(2)先求导数,求出函数的定义域,通过讨论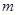 的正负,求导求单调区间.
的正负,求导求单调区间.
试题解析:(1)∵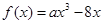 过点
过点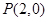
∴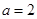 ,
,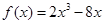 ,
(2分)
,
(2分)
∵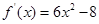 ,∴切线的斜率
,∴切线的斜率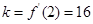 .
.
∵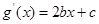 ,
,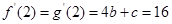 (1)
(1)
又∵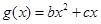 的图像过点
的图像过点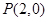 ∴
∴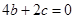 (2)
(2)
联立(1)(2)解得: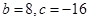 (4分)
(4分)
∴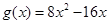 ;切线方程为
;切线方程为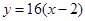 ,即
,即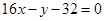
∴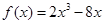 ,
,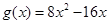 ;切线为:
;切线为: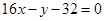 (6分)
(6分)
(2)∵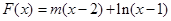 ,
,
∴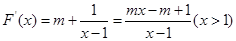 (9分)
(9分)
①当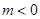 时,
时,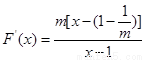 , ∵
, ∵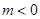 ,∴
,∴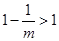
又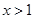 ,∴当
,∴当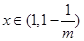 时,
时,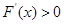 ;
;
当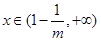 时,
时,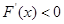 .
.
∴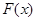 的单调减区间是
的单调减区间是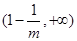 单调增区间是
单调增区间是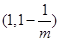 ; (11分)
; (11分)
②当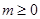 时,显然
时,显然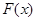 没有单调减区间,单调增区间是
没有单调减区间,单调增区间是 . (13分)
. (13分)
考点:1.利用导数求切线方程;2.利用导数求单调区间.

练习册系列答案
相关题目
 的图像过点(1,3),且
的图像过点(1,3),且 对任意实数都成立,函数
对任意实数都成立,函数 与
与 的图像关于原点对称.
的图像关于原点对称. 与
与 的解析式;
的解析式; 在[-1,1]上是增函数,求实数λ的取值范围.
在[-1,1]上是增函数,求实数λ的取值范围. 与
与 的图像都过点
的图像都过点 ,且在点
,且在点 处有公共切线,求
处有公共切线,求 、
、 的表达式。
的表达式。 的图像过点
的图像过点 ,且
,且 对任意实数都成
对任意实数都成 与
与 的图像关于原点对称.
的图像关于原点对称.  .
. 与
与 的解析式;
的解析式; 在[-1,1]上是增函数,求实数λ的取值范围.
在[-1,1]上是增函数,求实数λ的取值范围.