题目内容
在（1+x）5+（1+x）6+（1+x）7的展开式中，含x4项的系数是等差数列an=3n-5的（ ）A．第2项
B．第11项
C．第20项
D．第24项
【答案】分析：利用二项式展开式的通项公式，求得含 x4项的系数是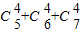
=55，可得含 x4项的系数是an=3n-5 的第20项．
解答：解：在（1+x）5+（1+x）6+（1+x）7 的展开式中，含 x4项的系数是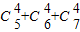
=55，
所以，含 x4项的系数是an=3n-5 的第20项，
故选C．
点评：本题主要考查二项式展开式的通项公式，二项式系数的性质、等差数列通项公式，属于中档题．
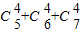=55，可得含 x4项的系数是an=3n-5 的第20项．解答：解：在（1+x）5+（1+x）6+（1+x）7 的展开式中，含 x4项的系数是
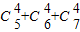=55，所以，含 x4项的系数是an=3n-5 的第20项，
故选C．
点评：本题主要考查二项式展开式的通项公式，二项式系数的性质、等差数列通项公式，属于中档题．
练习册系列答案
相关题目