Question

设A是三角形的内角，且sinA和cosA是关于x方程25x²﹣5ax﹣12a=0的两个根．

（1）求a的值；

（2）求tanA的值．

Answer 1

考点：

同角三角函数间的基本关系；函数的零点．

专题：

解三角形．

分析：

（1）根据一元二次方程根与系数的关系可得 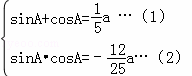，把（1）式两边平方，花简求得a的值．

（2）由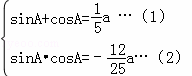，且sinA＞0，cosA＜0，求得cosA、sinA的值，即可求得tanA的值．

解答：

解：（1）因为sinA和cosA是关于x方程25x²﹣5ax﹣12a=0的两个根，所以由韦达定理得：．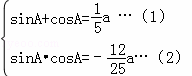

把（1）式两边平方，得，即 ，解得a=﹣25，或a=1．

当∴a=﹣25时，不合题意，所以a=1．

（2）由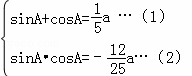，且sinA＞0，cosA＜0，可得 ，

∴．

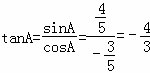点评：

本题主要考查一元二次方程根与系数的关系，同角三角函数的基本关系，属于基础题．