题目内容
16.x,y是整数,a>b>0,且a+b=10,$\frac{a}{x}+\frac{b}{y}$=1,x+y的最小值为18,则a,b的值分别是( )| A. | a=8,b=2 | B. | a=9,b=1 | C. | a=7,b=3 | D. | a=7,b=3 |
分析 由题意,x+y=(x+y)($\frac{a}{x}+\frac{b}{y}$)=a+b+$\frac{ay}{x}$+$\frac{bx}{y}$≥10+2$\sqrt{ab}$,利用x+y的最小值为18,可得2$\sqrt{ab}$=8,即可求出a,b的值.
解答 解:由题意,x+y=(x+y)($\frac{a}{x}+\frac{b}{y}$)=a+b+$\frac{ay}{x}$+$\frac{bx}{y}$≥10+2$\sqrt{ab}$,
∵x+y的最小值为18,
∴2$\sqrt{ab}$=8,
∵a+b=10,
∴a=8,b=2,
故选A.
点评 本题考查基本不等式的运用,考查“1”的代换,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
5.如图是一个几何体的三视图,则该几何体的体积是( )
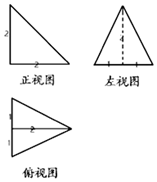

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
1.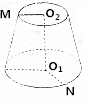 如图,圆台的高为4,上、下底面半径分别为3、5,M、N分别在上、下底面圆周上,且<$\overrightarrow{{O}_{2}M}$,$\overrightarrow{{O}_{1}N}$>=120°,则|$\overrightarrow{MN}$|等于( )
如图,圆台的高为4,上、下底面半径分别为3、5,M、N分别在上、下底面圆周上,且<$\overrightarrow{{O}_{2}M}$,$\overrightarrow{{O}_{1}N}$>=120°,则|$\overrightarrow{MN}$|等于( )
 如图,圆台的高为4,上、下底面半径分别为3、5,M、N分别在上、下底面圆周上,且<$\overrightarrow{{O}_{2}M}$,$\overrightarrow{{O}_{1}N}$>=120°,则|$\overrightarrow{MN}$|等于( )
如图,圆台的高为4,上、下底面半径分别为3、5,M、N分别在上、下底面圆周上,且<$\overrightarrow{{O}_{2}M}$,$\overrightarrow{{O}_{1}N}$>=120°,则|$\overrightarrow{MN}$|等于( )| A. | $\sqrt{65}$ | B. | 5$\sqrt{2}$ | C. | $\sqrt{35}$ | D. | 5 |
8.已知在正方体ABCD-A1B1C1D1中,E,F,G分别是AB,BB1,B1C1的中点,则过这三点的截面图的形状是( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
6.曲线y=ex+1在点A(0,2)处的切线斜率为( )
| A. | 1 | B. | 2 | C. | e | D. | $\frac{1}{e}$ |
 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥平面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC的中点,过MN作平面MNPQ分别与线段CD,AB相交于点P,Q,且$\overrightarrow{AQ}=λ\overrightarrow{AB}$.
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥平面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC的中点,过MN作平面MNPQ分别与线段CD,AB相交于点P,Q,且$\overrightarrow{AQ}=λ\overrightarrow{AB}$.