题目内容
16.设命题p:x≤$\frac{1}{2}$或x≥1,命题q:(x-a)(x-a-1)≤0,若p是¬q的必要不充分条件,求实数a的取值范围.分析 命题q:(x-a)(x-a-1)≤0,解得a≤x≤a+1,¬q为:x<a,或x>a+1.根据p是¬q的必要不充分条件,可得$a≤\frac{1}{2}$,且a+1≥1,即可得出.
解答 解:命题q:(x-a)(x-a-1)≤0,解得a≤x≤a+1,¬q为:x<a,或x>a+1.
又命题p:x≤$\frac{1}{2}$或x≥1,∵p是¬q的必要不充分条件,
∴$a≤\frac{1}{2}$,且a+1≥1,
解得$0≤a≤\frac{1}{2}$.
∴实数a的取值范围是$[0,\frac{1}{2}]$.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
7.已知函数f(x)是定义域R在上的奇函数,且在区间[0,+∞)单调递增,若实数a满足f(log2a)+f(log2$\frac{1}{a}$)≤2f(1),则a的取值范围是( )
| A. | (-∞,2] | B. | $({0,\frac{1}{2}}]$ | C. | $[{\frac{1}{2},2}]$ | D. | (0,2] |
11.由1,2,3这三个数字组成的没有重复数字的三位自然数共有( )
| A. | 6个 | B. | 8个 | C. | 12个 | D. | 15个 |
1.sin(-690°)的值为( )
| A. | $({\frac{{\sqrt{3}}}{2}})$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
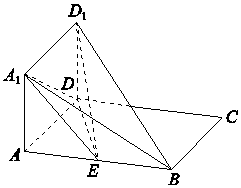 如图所示,四边形ABCD和四边形ADD1A1均为矩形且所在的平面互相垂直,E为线段AB的中点.
如图所示,四边形ABCD和四边形ADD1A1均为矩形且所在的平面互相垂直,E为线段AB的中点.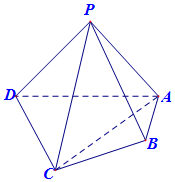 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.