Question

【题目】如图，四棱锥的底面是直角梯形，，⊥，△和△是两个边长为2的正三角形，．

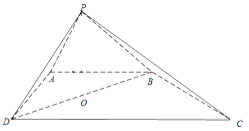
（1）求证：平面⊥平面；

（2）求二面角的余弦值．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题分析：（1）证明：易得，又，计算可得 ，又平面平面平面；（2）解：由（1）知平面，又建立坐标系求得：平面的法向量为，又平面的一个法向量为二面角的余弦值为．

试题解析：（1）证明：设是的中点，连接，

∵和是两个边长为的正三角形，∴，

又，∴，

∵，

∴在中，由勾股定理可得，，

∴，

在中，由勾股定理可得，

在中，．

在中，，由勾股定理的逆定理可得，

又∵，

∴平面，

∵平面，

∴平面平面．

（2）解：由（1）知平面，又．

∴过分别作，的平行线，以它们作，轴，以为轴建立如图所示的空间直角坐标系．

由已知得：，，，，，

则，，

设平面的法向量为，

则即解得令，

则平面的一个法向量为，又平面的一个法向量为，

则，

∴二面角的余弦值为．