题目内容
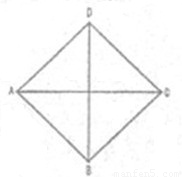
已知ABCD是空间四边形形,E、F、G、H分别是AB、BC、CD、DA的中点,如果对角线AC=4,BD=2,那么EG2+HF2的值等于
- A.10
- B.15
- C.20
- D.25
A
试题分析:依次连接EF、FG、GH、HE
∵E是AB中点,H是AD中点,∴EH∥BD,且EH=" BD=1"
同理:
FG∥BD,FG=" BD=1" ,所以,EH∥FG,EH=FG
同理,EF∥HG,EF=HG
所以,四边形EFGH为边长为1、2的平行四边形
设∠EHG=θ,那么∠HEF="180°-θ"
在△EHG中,由余弦定理有:
EG2="EH2+HG2-2×EH×HG×cosθ=1+4-4cosθ=5-4cosθ"
在△EFH中,由余弦定理有:
FH2=EF2+EH2-2×EF×EH×cos(180°-θ)=4+1-4cos(180°-θ)="5+4cosθ"
上述两式相加,得到:
EG2+FH2=5-4cosθ+5+4cosθ=10
故选A
考点:本题主要考查空间四边形中的线线平行关系及余弦定理的应用。
点评:注意把立体几何问题转化成平面问题,这里运用了余弦定理,对高一学生来说是个难题。
试题分析:依次连接EF、FG、GH、HE
∵E是AB中点,H是AD中点,∴EH∥BD,且EH=" BD=1"
同理:
FG∥BD,FG=" BD=1" ,所以,EH∥FG,EH=FG
同理,EF∥HG,EF=HG
所以,四边形EFGH为边长为1、2的平行四边形
设∠EHG=θ,那么∠HEF="180°-θ"
在△EHG中,由余弦定理有:
EG2="EH2+HG2-2×EH×HG×cosθ=1+4-4cosθ=5-4cosθ"
在△EFH中,由余弦定理有:
FH2=EF2+EH2-2×EF×EH×cos(180°-θ)=4+1-4cos(180°-θ)="5+4cosθ"
上述两式相加,得到:
EG2+FH2=5-4cosθ+5+4cosθ=10
故选A
考点:本题主要考查空间四边形中的线线平行关系及余弦定理的应用。
点评:注意把立体几何问题转化成平面问题,这里运用了余弦定理,对高一学生来说是个难题。

练习册系列答案
相关题目
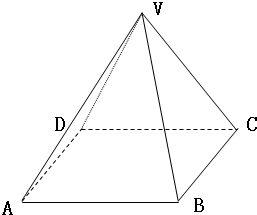 如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h. 我们将底面是正方形,侧棱长都相等的棱锥称为正四棱锥.已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同,且如图所示,视图中四边形ABCD是边长为1的正方形,则该几何体的体积为( )
我们将底面是正方形,侧棱长都相等的棱锥称为正四棱锥.已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同,且如图所示,视图中四边形ABCD是边长为1的正方形,则该几何体的体积为( )