题目内容
已知函数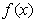 是定义在
是定义在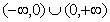 上的偶函数,当
上的偶函数,当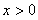 时,
时,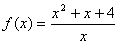
(1)求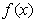 的解析式.
的解析式.
(2)讨论函数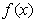 的单调性,并求
的单调性,并求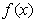 的值域.
的值域.
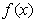 是定义在
是定义在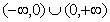 上的偶函数,当
上的偶函数,当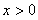 时,
时,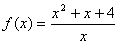
(1)求
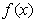 的解析式.
的解析式.(2)讨论函数
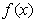 的单调性,并求
的单调性,并求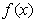 的值域.
的值域.见解析
解:(1) 当 则
则 ,
,
又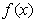 是偶函数所以
是偶函数所以

∴
(2)当 ;
;
当 单调递减,当
单调递减,当 单调递增。
单调递增。
又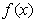 是偶函数,
是偶函数,
故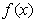 的单调递减区间为
的单调递减区间为 .单调递增区间为
.单调递增区间为
当
 ,当
,当 ,故
,故
又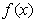 是偶函数,当
是偶函数,当

综上,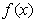 的值域为
的值域为
 则
则 ,
,又
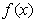 是偶函数所以
是偶函数所以

∴

(2)当
 ;
;当
 单调递减,当
单调递减,当 单调递增。
单调递增。又
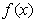 是偶函数,
是偶函数,故
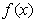 的单调递减区间为
的单调递减区间为 .单调递增区间为
.单调递增区间为
当

 ,当
,当 ,故
,故
又
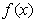 是偶函数,当
是偶函数,当

综上,
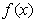 的值域为
的值域为

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,若
,若 ,试求:
,试求: 的值;
的值; 的值.
的值. 5)等于( )
5)等于( ) 是奇函数,且在
是奇函数,且在 内是增函数,又
内是增函数,又 ,则
,则 的解集是( )
的解集是( ) ;
;
 ;
;

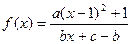 (
(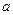 、b、
、b、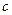 ∈N)的图像按向量
∈N)的图像按向量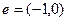 平移后得到的图 像关于原点对称,且
平移后得到的图 像关于原点对称,且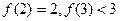 .
.
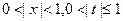 ,求证:
,求证: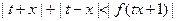 ;
;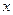 是正实数,求证:
是正实数,求证: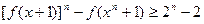 .
.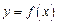 满足:①
满足:①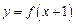 是偶函数;②在
是偶函数;②在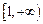 上为增函数。若
上为增函数。若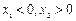 ,且
,且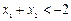 ,则
,则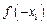 与
与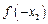 的大小关系是( )
的大小关系是( )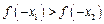

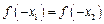
 的图象关于直线
的图象关于直线 对称,且当
对称,且当 时,
时,
 则当
则当 时,
时, 的解析式为( )
的解析式为( )



 是奇函数,则实数
是奇函数,则实数 =_________
=_________