题目内容
已知函数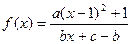 (
(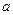 、b、
、b、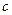 ∈N)的图像按向量
∈N)的图像按向量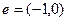 平移后得到的图 像关于原点对称,且
平移后得到的图 像关于原点对称,且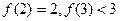 .
.
(1)求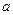 ,b,
,b,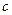 的值;
的值;
(2)设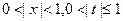 ,求证:
,求证: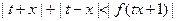 ;
;
(3)设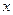 是正实数,求证:
是正实数,求证: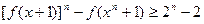 .
.
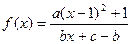 (
(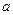 、b、
、b、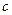 ∈N)的图像按向量
∈N)的图像按向量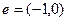 平移后得到的图 像关于原点对称,且
平移后得到的图 像关于原点对称,且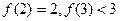 .
.
(1)求
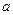 ,b,
,b,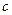 的值;
的值;
(2)设
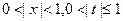 ,求证:
,求证: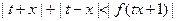 ;
;
(3)设
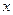 是正实数,求证:
是正实数,求证: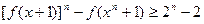 .
.
(1)函数 的图像按
的图像按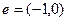 平移后得到的图像所对应的函数式为
平移后得到的图像所对应的函数式为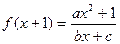 .
.
∵函数 的图像平移后得到的图像关于原点对称,
的图像平移后得到的图像关于原点对称,
∴ ,即
,即 .
.
∵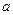 ∈N,∴
∈N,∴ .∴
.∴ ,∴c=0.
,∴c=0.
又∵ ,∴
,∴ .∴
.∴ ,∴
,∴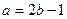 . ①
. ①
又 .∴
.∴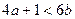 . ②
. ②
由①,②及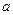 、
、 N,得
N,得 .
.
(2)∴ ,∴
,∴ .
.
∴ ,当且仅当
,当且仅当 时,上式取等号.
时,上式取等号.
但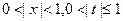 ,∴
,∴ ,
,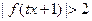 .
.
由于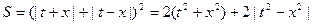 ,
,
当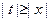 时,
时, ≤4;当
≤4;当 时,S
时,S <4.
<4.
∴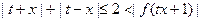 ,即
,即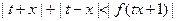 .
.
(3) =1时,结论显然成立.
=1时,结论显然成立.
当n≥2时,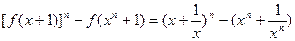

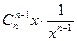


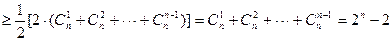 .
.
 的图像按
的图像按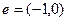 平移后得到的图像所对应的函数式为
平移后得到的图像所对应的函数式为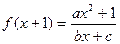 .
.∵函数
 的图像平移后得到的图像关于原点对称,
的图像平移后得到的图像关于原点对称,∴
 ,即
,即 .
.∵
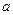 ∈N,∴
∈N,∴ .∴
.∴ ,∴c=0.
,∴c=0.又∵
 ,∴
,∴ .∴
.∴ ,∴
,∴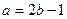 . ①
. ①又
 .∴
.∴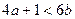 . ②
. ②由①,②及
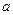 、
、 N,得
N,得 .
.(2)∴
 ,∴
,∴ .
.∴
 ,当且仅当
,当且仅当 时,上式取等号.
时,上式取等号.但
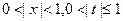 ,∴
,∴ ,
,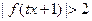 .
.由于
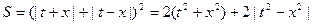 ,
,当
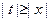 时,
时, ≤4;当
≤4;当 时,S
时,S <4.
<4.∴
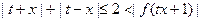 ,即
,即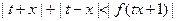 .
.(3)
 =1时,结论显然成立.
=1时,结论显然成立.当n≥2时,
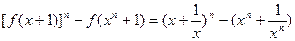

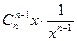


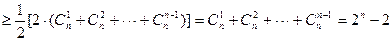 .
. (1)函数 的图像按
的图像按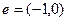 平移后得到的图像所对应的函数式为
平移后得到的图像所对应的函数式为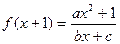 .
.
∵函数 的图像平移后得到的图像关于原点对称,
的图像平移后得到的图像关于原点对称,
∴ ,即
,即 .
.
∵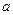 ∈N,∴
∈N,∴ .∴
.∴ ,∴c=0.
,∴c=0.
又∵ ,∴
,∴ .∴
.∴ ,∴
,∴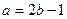 . ①
. ①
又 .∴
.∴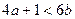 . ②
. ②
由①,②及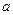 、
、 N,得
N,得 .
.
(2)∴ ,∴
,∴ .
.
∴ ,当且仅当
,当且仅当 时,上式取等号.
时,上式取等号.
但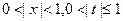 ,∴
,∴ ,
,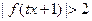 .
.
由于 ,
,
当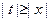 时,
时, ≤4;当
≤4;当 时,S
时,S <4.
<4.
∴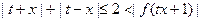 ,即
,即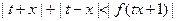 .
.
(3) =1时,结论显然成立.
=1时,结论显然成立.
当n≥2时,
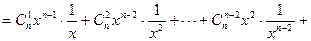
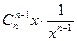
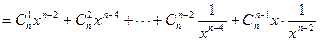

 .
.
 的图像按
的图像按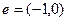 平移后得到的图像所对应的函数式为
平移后得到的图像所对应的函数式为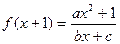 .
.∵函数
 的图像平移后得到的图像关于原点对称,
的图像平移后得到的图像关于原点对称,∴
 ,即
,即 .
.∵
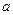 ∈N,∴
∈N,∴ .∴
.∴ ,∴c=0.
,∴c=0.又∵
 ,∴
,∴ .∴
.∴ ,∴
,∴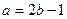 . ①
. ①又
 .∴
.∴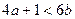 . ②
. ②由①,②及
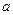 、
、 N,得
N,得 .
.(2)∴
 ,∴
,∴ .
.∴
 ,当且仅当
,当且仅当 时,上式取等号.
时,上式取等号.但
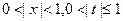 ,∴
,∴ ,
,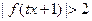 .
.由于
 ,
,当
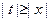 时,
时, ≤4;当
≤4;当 时,S
时,S <4.
<4.∴
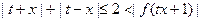 ,即
,即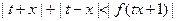 .
.(3)
 =1时,结论显然成立.
=1时,结论显然成立.当n≥2时,

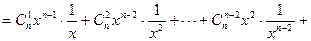
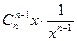
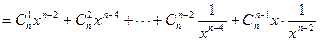

 .
.
练习册系列答案
相关题目
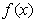 是定义在
是定义在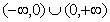 上的偶函数,当
上的偶函数,当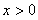 时,
时,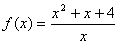
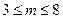 。另外,年销售
。另外,年销售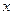 件B产品时需上交
件B产品时需上交 万美元的特别关税。
万美元的特别关税。 ,
,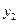 与生产相应产品的件数
与生产相应产品的件数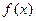 是R上的函数,且满足
是R上的函数,且满足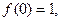 并且对任意的实数
并且对任意的实数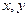 都有
都有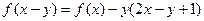 ,求
,求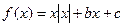 ,给出四个命题:
,给出四个命题: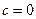 时,有
时,有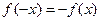 成立;
成立;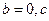 ﹥0时,方程
﹥0时,方程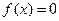 ,只有一个实数根;
,只有一个实数根;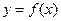 的图象关于点(0,c)对称;
的图象关于点(0,c)对称;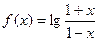 ,
,
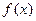 的定义域;
的定义域;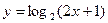 的图像向右平移1个单位可以得到函数的解析式是 。
的图像向右平移1个单位可以得到函数的解析式是 。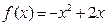 ,则对任意实数
,则对任意实数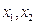 ,下列不等式总成立的是( )
,下列不等式总成立的是( )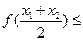
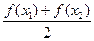
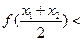
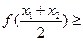
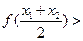
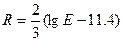 .2008年5月12日,中国汶川发生了8.0级特大地震,而1989年旧金山海湾区域地震的震级为6.0级,那么2008年地震的能量是1989年地震能量的 倍.
.2008年5月12日,中国汶川发生了8.0级特大地震,而1989年旧金山海湾区域地震的震级为6.0级,那么2008年地震的能量是1989年地震能量的 倍.