题目内容
已知函数 .
.
⑴若 ,解方程
,解方程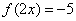 ;
;
⑵若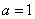 ,判断
,判断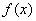 的单调区间并证明;
的单调区间并证明;
⑶若存在实数 ,使
,使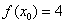 ,求实数
,求实数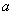 的取值范围 .
的取值范围 .
⑴若 , 由
, 由 ,即
,即 ,解得
,解得
⑵若 ,则
,则 ,设
,设 ,且
,且 ,
,






① 当 时,有
时,有 ,
, ,
,
 ,
, 在
在 上是增函数;
上是增函数;
② 当 时,有
时,有 ,
, ,
,
 ,
, 在
在 上是减函数
上是减函数
 的单调增区间是
的单调增区间是 ,单调减区间是
,单调减区间是
⑶设 ,由
,由 ,得
,得 ,且
,且
 存在
存在 ,使得
,使得 ,即
,即
令 ,若
,若 ,则函数
,则函数 的对称轴是
的对称轴是
由已知得:方程 在
在 上有实数解,
上有实数解,
 ,或
,或
由不等式 得:
得:
由不等式组 得:
得: 
所以,实数 的取值范围是
的取值范围是

练习册系列答案
相关题目
 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合). ,若存在常数
,若存在常数 ,对任意
,对任意 ,存在唯一
,存在唯一 的,使得
的,使得 ,则称函数
,则称函数 上的均值为
上的均值为 ,则函数
,则函数 在
在 上的均值为。
上的均值为。 B.
B. 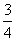 C.
C.  D.
D. 
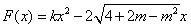 ,
,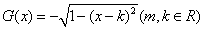
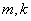 是常数,问当
是常数,问当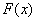 有最大值,并求出
有最大值,并求出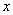 的值;
的值;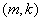 同时满足条件:(甲)
同时满足条件:(甲)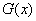 取最小值的
取最小值的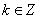 ?
?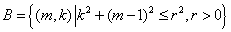 ,求使
,求使 的
的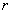 的取值范围。
的取值范围。 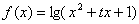 (
(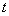 为常数,且
为常数,且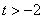 ).
).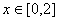 时,求函数
时,求函数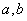 使得
使得 ,
,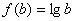 ,并且
,并且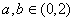 ,若存在,求出实数
,若存在,求出实数 ,当
,当 变化时,
变化时, 恒成立,则实数
恒成立,则实数 的取值范围是___________.
的取值范围是___________. 的值域为
的值域为 ,则m+n=__________.
,则m+n=__________.  =
= tan
tan -
- sin
sin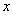 +4(其中
+4(其中
 0),如果
0),如果 ,则
,则 (2010
(2010 -3)的值为 ( )
-3)的值为 ( ) 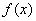 是周期为2的奇函数,当
是周期为2的奇函数,当 时,
时,
 ,则
,则