题目内容
（1）计算：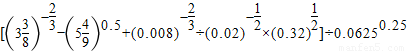
；（2）求不等式x2-6|x|+5≤0的解．
【答案】分析：（1）利用指数幂的运算性质即可化简出答案；
（2）由x2=|x|2，因此可把原不等式看作关于|x|的一元二次不等式，解出即可．
解答：解：（1）原式=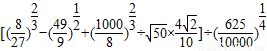
=
÷
=
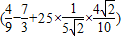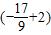×2=
．
（2）x2-6|x|+5≤0?|x|2-6|x|+5≤0?（|x|-1）（|x|-5）≤0，
?1≤|x|≤5，
解得-5≤x≤-1，或1≤x≤5．
点评：熟练掌握指数幂的运算法则和转化为关于|x|的一元二次不等式是解题的关键．
（2）由x2=|x|2，因此可把原不等式看作关于|x|的一元二次不等式，解出即可．
解答：解：（1）原式=
=
÷=
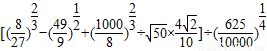
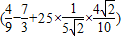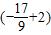×2=．（2）x2-6|x|+5≤0?|x|2-6|x|+5≤0?（|x|-1）（|x|-5）≤0，
?1≤|x|≤5，
解得-5≤x≤-1，或1≤x≤5．
点评：熟练掌握指数幂的运算法则和转化为关于|x|的一元二次不等式是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
（1）计算：0.25-2-8