Question

函数f（x）=kx²-

|x|

x+4

（k∈R）的零点个数最多是（　　）

A．1

B．2

C．3

D．4

Answer 1

函数f（x）=kx²-

|x|

x+4

（k∈R）零点的个数，
即为函数y=kx²与y=

|x|

x+4

的图象交点个数，
在同一坐标系内分别作出函数y=kx²与y=

|x|

x+4

的图象，



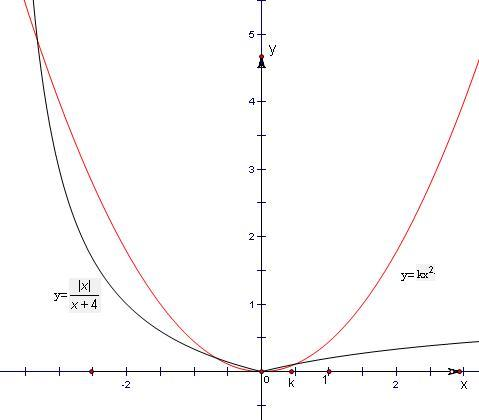
知两函数图象最多有4个交点，
即函数f（x）=kx²-

|x|

x+4

（k∈R）的零点个数最多是4．
故选D．