题目内容
如图所示为函数f（x）=x3+bx2+cx+d的导函数f′（x）的图象，则函数
的单调减区间为
- A.
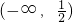
- B.
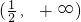
- C.（3，+∞）
- D.（-∞，-2）
C
分析：求导函数可得f′（x）=3x2+2bx+c，根据图象可知-2，3是3x2+2bx+c=0的两根，求出b，c，再确定函数的定义域，利用对数函数为减函数，即可求得结论．
解答：求导函数可得f′（x）=3x2+2bx+c，根据图象可知-2，3是3x2+2bx+c=0的两根
∴
，
∴
∴=
由x2-x-6＞0，可得函数的定义域为（-∞，-2）∪（3，+∞）
又
，对数函数
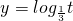在定义域内为减函数
∴函数的单调减区间为（3，+∞）
故选C．
点评：本题考查复合函数的单调性，考查导函数的图象，考查学生分析解决问题的能力，属于中档题．
分析：求导函数可得f′（x）=3x2+2bx+c，根据图象可知-2，3是3x2+2bx+c=0的两根，求出b，c，再确定函数的定义域，利用对数函数为减函数，即可求得结论．
解答：求导函数可得f′（x）=3x2+2bx+c，根据图象可知-2，3是3x2+2bx+c=0的两根
∴
，∴
∴
=由x2-x-6＞0，可得函数的定义域为（-∞，-2）∪（3，+∞）
又
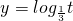，对数函数在定义域内为减函数∴函数
的单调减区间为（3，+∞）故选C．
点评：本题考查复合函数的单调性，考查导函数的图象，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，
（2012•佛山二模）如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）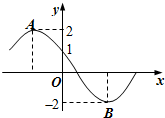
如图所示为函数f（x）=Asin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）
如图所示为函数f（x）=2cos（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中
（2012•广安二模）如图所示为函数f（x）=x3+bx2+cx+d的导函数f′（x）的图象，则函数