题目内容
如图所示为函数f（x）=2cos（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中|| AB |
分析：先确定函数的周期，由图可知|
|=5，AB间的纵向距离为4，故可由勾股定理计算AB间的横向距离，即半个周期，进而得ω值，再利用函数图象过点（0，1），且此点在减区间上，代入函数解析式即可计算φ值．然后利用定积分求出区域面积．
| AB |
解答：解：由图可知函数的振幅为2，半周期为AB间的横向距离，
=
=3，
∴T=6，即
=6
∴ω=
由图象知函数过点（0，1）
∴1=2cosφ
∴φ=2kπ+
，k∈Z
∵0≤φ≤π
∴φ=
，函数的解析式为：f（x）=2cos（
x+
），A（-1，2），B（2，-2）
直线AB的方程：
=
，即y=-
x+
，
直线AB与函数f（x）的图象围成的封闭图形的面积为2
[2cos(
x+
)+
x-
]dx
=2[
sin(
x+
) +
x2-
x]
=2[
sin(
×
+
) +
(
)2-
×
]-2[
sin(
×(-1)+
) +
(-1)2-
×(-1)]
=
-3．
故选B．
| T |
| 2 |
| 52-42 |
∴T=6，即
| 2π |
| ω |
∴ω=
| π |
| 3 |
由图象知函数过点（0，1）
∴1=2cosφ
∴φ=2kπ+
| π |
| 3 |
∵0≤φ≤π
∴φ=
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
直线AB的方程：
| y-2 |
| 2+2 |
| x+1 |
| -1-2 |
| 4 |
| 3 |
| 2 |
| 3 |
直线AB与函数f（x）的图象围成的封闭图形的面积为2
| ∫ |
-1 |
| π |
| 3 |
| π |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
=2[
| 6 |
| π |
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| | |
-1 |
=2[
| 6 |
| π |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 6 |
| π |
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
=
| 12 |
| π |
故选B．
点评：本题考查了三角函数的图象和性质，由y=Asin（ωx+φ）的部分图象确定其解析式的方法，三角函数周期的求法，定积分的求法．考查计算能力．
练习册系列答案
相关题目
如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，
（2012•佛山二模）如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）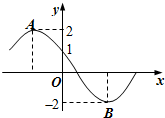
如图所示为函数f（x）=Asin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）
（2012•广安二模）如图所示为函数f（x）=x3+bx2+cx+d的导函数f′（x）的图象，则函数