题目内容
【题目】已知函数f (x)=![]() (a≠0).
(a≠0).
(1)当a=-1,b=0时,求函数f (x)的极值;
(2)当b=1时,若函数f (x)没有零点,求实数a的取值范围.
【答案】(1)极小值为![]() ,无极大值; (2)
,无极大值; (2)![]() .
.
【解析】
(1)当![]() 时,求得函数的导数,利用导数求得函数的单调性,结合函数极值的定义,即可求解;
时,求得函数的导数,利用导数求得函数的单调性,结合函数极值的定义,即可求解;
(2)把函数![]() 没有零点,转化为方程ax-a+ex=0无实根,令
没有零点,转化为方程ax-a+ex=0无实根,令![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与最值,列出不等式,即可求解.
的单调性与最值,列出不等式,即可求解.
(1)当![]() 时,函数
时,函数![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增.
单调递增.
所以![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
(2)当![]() 时,函数
时,函数![]() ,
,
因为函数![]() 没有零点,即方程
没有零点,即方程![]() 无实根,即ax-a+ex=0无实根,
无实根,即ax-a+ex=0无实根,
令![]() ,则
,则![]() ,
,
若![]() 时,则
时,则![]() 在R上单调递增,
在R上单调递增,![]() 此时存在
此时存在![]() ,使得
,使得![]() ,不合题意;
,不合题意;
若![]() 时,令
时,令![]() ,即
,即![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() ,
,
所以当![]() ,函数
,函数![]() 取得最小值,最小值为
取得最小值,最小值为![]() ,
,
![]() 要使得函数
要使得函数![]() 没有零点,则满足
没有零点,则满足![]() ,即
,即![]() ,
,
解得![]() ,
,
综上所述,实数的取值范围为![]() .
.

 53随堂测系列答案
53随堂测系列答案【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有![]() 的把握认为男、女顾客对该商场服务的评价有差异?
的把握认为男、女顾客对该商场服务的评价有差异?
【题目】某市工业部门计划对所辖中小型企业推行节能降耗技术改造,下面是对所辖企业是否支持技术改造进行的问卷调查的结果:
支持 | 不支持 | 合计 | |
中型企业 | 40 | ||
小型企业 | 240 | ||
合计 | 560 |
已知从这560家企业中随机抽取1家,抽到支持技术改造的企业的概率为![]() .
.
(1)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?
(2)从支持节能降耗的中小企业中按分层抽样的方法抽出8家企业,然后从这8家企业选出2家进行奖励,分别奖励中型企业20万元,小型企业10万元.求奖励总金额为20万元的概率.
附:![]()
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
【题目】交通部门调查在高速公路上的平均车速情况,随机抽查了60名家庭轿车驾驶员,统计其中有40名男性驾驶员,其中平均车速超过![]() 的有30人,不超过
的有30人,不超过![]() 的有10人;在其余20名女性驾驶员中,平均车速超过
的有10人;在其余20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(1)完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为,家庭轿车平均车速超过
的把握认为,家庭轿车平均车速超过![]() 与驾驶员的性别有关;
与驾驶员的性别有关;
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶员 | |||
女性驾驶员 | |||
合计 |
(2)根据这些样本数据来估计总体,随机调查3辆家庭轿车,记这3辆车中,驾驶员为女性且平均车速不超过![]() 的人数为
的人数为![]() ,假定抽取的结果相互独立,求
,假定抽取的结果相互独立,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: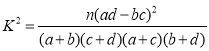
![]()
临界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |