题目内容
12.已知函数f(x)=ax(x+1)-lnx.(1)当a=1时,求f(x)在(1,f(1))处的切线方程;
(2)若函数g(x)=f(x)+lnx-ax2+ex,当a<-1时,求g(x)的极值.
分析 (1)求得导数,求得切线的斜率和切点,由点斜式方程可得切线的方程;
(2)求得g(x)的导数,令导数大于0,可得增区间;由导数小于0,可得减区间,进而得到极值.
解答 解:(1)当a=1,f(x)=x(x+1)-lnx=x2+x-lnx,
f(1)=1+1-ln1=2,∴切点坐标为(1,2),
$f'(x)=2x+1-\frac{1}{x}$,∴k=f'(1)=2+1-1=2.
根据直线的点斜式方程,切线方程为y-2=2(x-1),
∴f(x)在(1,f(1))处的切线方程2x-y=0;
(2)依题意得,g(x)=ax2+ax-lnx+lnx-ax2+ex=ax+ex
g'(x)=a+ex,由ex>-a,
∵a<-1,∴-a>1,解得x>ln(-a),
∴f(x)在(ln(-a),+∞)上单调递增,
在(0,ln(-a))上单调递减.
∴$g{(x)_{极小值}}=g(ln(-a))=aln(-a)+{e^{ln(-a)}}=-a+aln(-a)$,g(x)无极大值.
点评 本题考查导数的运用:求切线的方程和单调区间、极值,考查运算能力,正确求出导数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设x>y>0,则下列各式中正确的是( )
| A. | x>$\frac{x+y}{2}$>$\sqrt{xy}$>y | B. | y>$\frac{x+y}{2}$>$\sqrt{xy}$>x | C. | x>$\frac{x+y}{2}$>y>$\sqrt{xy}$ | D. | y>$\frac{x+y}{2}$≥$\sqrt{xy}$>x |
17.下列函数中,对于任意x∈R,同时满足条件f(x)=f(-x)和f(x-π)=f(x)的函数是( )
| A. | f(x)=sinx | B. | f(x)=sinx•cosx | C. | f(x)=cosx | D. | f(x)=cos2x-sin2x |
1.定积分$\int_{-2π}^{2π}{({2x-sinx})}$的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
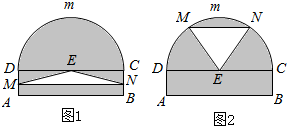 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定