题目内容
一元二次方程
有一个正根和一个负根的充分不必要条件是（ ）
A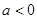． | B． | C． | D． |
C
解析试题分析：一元二次方程有一个正根和一个负根，根据韦达定理，得到成立的充要条件是：
，因为是充分不必要条件是C.
考点：1.充要条件；2.韦达定理.
练习册系列答案
相关题目
已知
，
，且
，则
的值（ ）
A． 或 | B．或 | C． | D． |
已知函数y＝
的定义域为A，集合B＝{x||x－3|＜a, a＞0}，若A∩B中的最小元素为2，则实数a的取值范围是：（ ）
| A．（0, 4] | B．（0, 4） | C．（1, 4] | D．（1, 4） |
，
，则
已知
，则“
”是“
”的
| A．充分而不必要条件 |
| B．必要而不充分条件 |
| C．充要条件 |
| D．既不充分也不必要条件 |
若
是两个非零的平面向量，则 “
”是“
”的
| A．充分且不必要条件 |
| B．必要且不充分条件 |
| C．充要条件 |
| D．既不充分也不必要条件 |
设p：
，q:
，若q是p的必要而不充分条件，
则实数a的取值范围是（ ）
A． | B． | C． | D． |
设
的
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
下列函数中，与函数
的奇偶性相同，且在
上单调性也相同的是
A． | B． |
C． | D． |