题目内容
经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位:L)与速度v(单位:km/h)的关系近似地满足u=
除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果的费用为y(元)(不计返程费用),将y表示成速度v的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
|
(1)设运送这车水果的费用为y(元)(不计返程费用),将y表示成速度v的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
分析:(1)由题意,当0<v≤50时,y=7.5•
μ+300•
=
+690,当v>50时,y=7.5•
μ+300•
=
+
+600,由此能将y表示成速度v的函数关系式.
(2)当0<v≤50时,y=
+690是单调减函数,故v=50时,y取得最小值ymin=
+690=3150,当v>50时,y=
+
+600,由导数求得当v=100时,y取得最小值ymin=
+
+600=2400,由于3150>2400,知当卡车以100km/h的速度行驶时,运送这车水果的费用最少.
| 400 |
| 100 |
| 400 |
| v |
| 123000 |
| v |
| 400 |
| 100 |
| 400 |
| v |
| 3v2 |
| 50 |
| 120000 |
| v |
(2)当0<v≤50时,y=
| 123000 |
| v |
| 123000 |
| v |
| 3v2 |
| 50 |
| 120000 |
| v |
| 3×1002 |
| 50 |
| 120000 |
| 100 |
解答:解:(1)由题意,当0<v≤50时,
y=7.5•
μ+300•
=30•(
+23)+300•
=
+690,
当v>50时,y=7.5•
μ+300•
=30(
+20)+300•
=
+
+600,
∴y=
.
(2)当0<v≤50时,
y=
+690是单调减函数,
故v=50时,y取得最小值ymin=
+690=3150,
当v>50时,y=
+
+600,
由y′=
-
=
=0,
得v=100.
当50<v<100时,y′<0,
函数y=
+
+600单调递增,
∴当v=100时,y取得最小值ymin=
+
+600=2400,
由于3150>2400,
所以,当v=100时,y取得最小值.
答:当卡车以100km/h的速度行驶时,运送这车水果的费用最少.
y=7.5•
| 400 |
| 100 |
| 400 |
| v |
=30•(
| 100 |
| v |
| 400 |
| v |
=
| 123000 |
| v |
当v>50时,y=7.5•
| 400 |
| 100 |
| 400 |
| v |
=30(
| v2 |
| 500 |
| 40 |
| v |
=
| 3v2 |
| 50 |
| 120000 |
| v |
∴y=
|
(2)当0<v≤50时,
y=
| 123000 |
| v |
故v=50时,y取得最小值ymin=
| 123000 |
| v |
当v>50时,y=
| 3v2 |
| 50 |
| 120000 |
| v |
由y′=
| 3v |
| 25 |
| 120000 |
| v2 |
| 3( v3-10 6) |
| 25v2 |
得v=100.
当50<v<100时,y′<0,
函数y=
| 3v2 |
| 50 |
| 120000 |
| v |
∴当v=100时,y取得最小值ymin=
| 3×1002 |
| 50 |
| 120000 |
| 100 |
由于3150>2400,
所以,当v=100时,y取得最小值.
答:当卡车以100km/h的速度行驶时,运送这车水果的费用最少.
点评:本题考查利用导数求闭区间上函数的最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.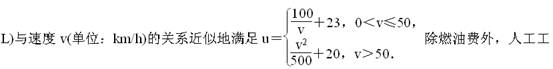
 除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元. 除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.