Question

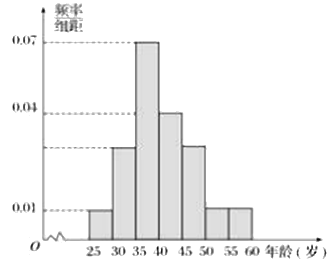
【题目】为选拔参加“全市高中数学竞赛”的选手，某中学举行了一次“数学竞赛”活动.为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为分）作为样本（样本容量为）进行统计.按照的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在的数据）.

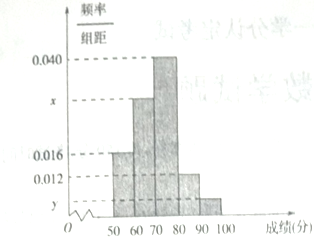
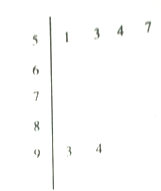
（1）求样本容和频率分布直方图中的值并求出抽取学生的平均分；

（2）在选取的样本中，从竞赛成绩在分以上（含分)的学生中随机抽取名学生参加“全市中数学竞赛”求所抽取的名学生中至少有一人得分在内的概率.

Answer 1

【答案】(1) ;(2) .

【解析】试题分析：（1）由样本容量和频数频率的关系易得答案；（2）由题意可知，分数在内的学生有3人，分数在内的学生有2人，抽取的2名学生的所有情况有种，其中2名同学的分数至少有一名得分在内的情况有7种，即可求所抽取的2名学生中至少有一人得分在内的概率.

试题解析：（1）由题意可知，样本容量 .

(2)由题意可知,分数在内的学生有 人,分数在 内的学生有 人,抽取的 名学生的所有情况有 种, 其中 名同学的分数至少有一名得分在 内的情况有 种,∴所抽取的 名学生中至少有一人得分在内的概率为.