题目内容
用数学归纳法证明: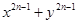 (
(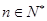 )能被
)能被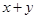 整除.从假设
整除.从假设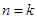 成立
成立
到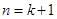 成立时,被整除式应为( )
成立时,被整除式应为( )
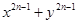 (
(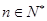 )能被
)能被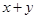 整除.从假设
整除.从假设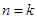 成立
成立到
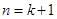 成立时,被整除式应为( )
成立时,被整除式应为( )A.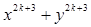 | B.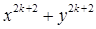 | C.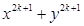 | D.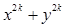 |
B
解:因为用数学归纳法证明: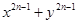 (
(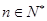 )能被
)能被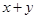 整除.从假设
整除.从假设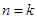 成立
成立
到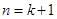 成立时,被整除式应为
成立时,被整除式应为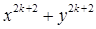 选B
选B
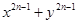 (
(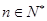 )能被
)能被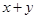 整除.从假设
整除.从假设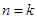 成立
成立到
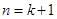 成立时,被整除式应为
成立时,被整除式应为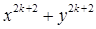 选B
选B
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
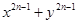 (
(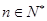 )能被
)能被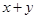 整除.从假设
整除.从假设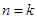 成立
成立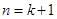 成立时,被整除式应为( )
成立时,被整除式应为( )A.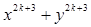 | B.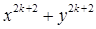 | C.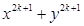 | D.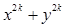 |
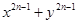 (
(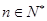 )能被
)能被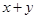 整除.从假设
整除.从假设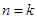 成立
成立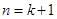 成立时,被整除式应为
成立时,被整除式应为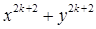 选B
选B
 名校课堂系列答案
名校课堂系列答案