题目内容
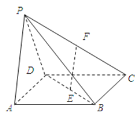
【题目】如图所示的四棱锥
中，底面
与侧面
垂直，且四边形
为正方形， 
，点
为边
的中点，点
在边
上，且
，过
， 
， 
三点的截面与平面
的交线为
，则异面直线
与
所成的角为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】因为
为边
的中点，连接
与DA的延长线交于点H，则A为DH的中点，所以有AD=AH.连接FE与PA的延长线交于点G，则直线GH即为过C，E，F三点的截面与平面PAD的交线
.
取PB的中点O，连接OE，AO.因为
，所以
.
所以F为
的中点，所以FE//OA,即FG//OA.
又易知OE//PA.即 OE∥AG.
所以四边形OEGA为平行四边形，从而
.
过点D作DM∥GH交PA于点M.则
，
从而得到
.即M为PA的中点.又DA=DP.因此DM⊥PA.
又底面ABCD与侧面PAD垂直，四边形ABCD为正方形，
所以AB⊥平面PAD.从而AB⊥DM.
因此DM⊥平面PAB.又DM//GH.即DM∥l.所以l⊥平面PAB.故l⊥PB，
所以异面直线PB与l所成的角为
.
本题选择D选项.
练习册系列答案
相关题目
