题目内容
有一抛物线形拱桥,中午12点时,拱顶离水面2米,桥下的水面宽4米;下午2点,水位下降了1米,桥下的水面宽
2
| 6 |
2
米.| 6 |
分析:由题设条件,设抛物线方程为x2=-2py,利用拱顶离水面2米,桥下的水面宽4米,得到抛物线方程为x2=-2py过点(2,-2),由此求出抛物线方程后能求出水面宽.
解答:解:设抛物线方程为x2=-2py,
∵拱顶离水面2米,桥下的水面宽4米,
∴抛物线方程为x2=-2py过点(2,-2),
所以p=1,x2=-2y,
当y=-3时,x=±
,
所以桥下的水面宽2
米.
故答案为:2
.
∵拱顶离水面2米,桥下的水面宽4米,
∴抛物线方程为x2=-2py过点(2,-2),
所以p=1,x2=-2y,
当y=-3时,x=±
| 6 |
所以桥下的水面宽2
| 6 |
故答案为:2
| 6 |
点评:本题考查抛物线的应用,解题时要认真审题,仔细解答,注意分析题设中的数量关系,合理地建立抛物线方程.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
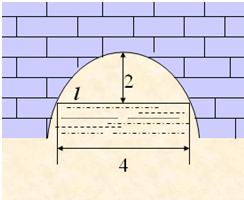 图中是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.
图中是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.
