题目内容
已知椭圆C:(1)证明λ=1-e2;
(2)确定λ的值,使得△PF1F2是等腰三角形.
(1)证明∵A、B是直线l:y=ex+a与x轴、y轴的交点,∴A、B的坐标分别为A(-![]() ,0)、B(0,a).
,0)、B(0,a).
由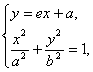
得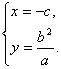 (c=
(c=![]() )∴M(-c,
)∴M(-c,![]() ).
).
由![]() =λ
=λ![]() ,得(-c+
,得(-c+![]() ,
,![]() )=λ(
)=λ(![]() ,a),
,a),
即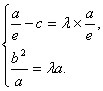
解得λ=1-e2.
(2)解:∵PF1⊥l,∴∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,即![]() |PF1|=c.
|PF1|=c.
依题意,点F1到l的距离为c,即![]() =c.
=c.
∴![]() =e,e2=
=e,e2=![]() ,λ=1-e2=
,λ=1-e2=![]() ,
,
即当λ=![]() 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.

练习册系列答案
相关题目
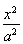



 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,且椭圆经过点N(2,-3).
,且椭圆经过点N(2,-3).