题目内容
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,点B是椭圆C的上顶点,点Q在椭圆C上(异于B点).
,点B是椭圆C的上顶点,点Q在椭圆C上(异于B点).
(Ⅰ)若椭圆V过点(﹣ ![]() ,
, ![]() ),求椭圆C的方程;
),求椭圆C的方程;
(Ⅱ)若直线l:y=kx+b与椭圆C交于B、P两点,若以PQ为直径的圆过点B,证明:存在k∈R, ![]() =
= ![]() .
.
【答案】解:(Ⅰ)椭圆的离心率e= ![]() =
= ![]() =
= ![]() ,则a2=2b2 ,
,则a2=2b2 ,
将点(﹣ ![]() ,
, ![]() )代入椭圆方程
)代入椭圆方程 ![]() ,解得:a2=4,b2=2,
,解得:a2=4,b2=2,
∴椭圆的标准方程为: ![]() ,
,
(Ⅱ)由题意的对称性可知:设存在存在k>0,使得 ![]() =
= ![]() ,
,
由a2=2b2 , 椭圆方程为: ![]() ,
,
将直线方程代入椭圆方程,整理得:(1+2k2)x2+4kbx=0,
解得:xP=﹣ ![]() ,则丨BP丨=
,则丨BP丨= ![]() ×
× ![]() ,
,
由BP⊥BQ,则丨BQ丨= ![]() ×丨
×丨 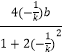 丨=
丨= ![]()
![]() ,
,
由 ![]() =
= ![]() .,则2
.,则2 ![]() ×
× ![]() =
= ![]()
![]() ,
,
整理得:2k3﹣2k2+4k﹣1=0,
设f(x)=2k3﹣2k2+4k﹣1,由f( ![]() )<0,f(
)<0,f( ![]() )>0,
)>0,
∴函数f(x)存在零点,
∴存在k∈R, ![]() =
= ![]()
【解析】(Ⅰ)由椭圆的离心率公式求得a和b的关系,将(﹣ ![]() ,
, ![]() )代入椭圆方程,即可求得a和b的值,求得椭圆方程;(Ⅱ)将直线方程代入椭圆方程,求得P的横坐标,求得丨BP丨,利用直线垂直的斜率关系求得丨BQ丨,由
)代入椭圆方程,即可求得a和b的值,求得椭圆方程;(Ⅱ)将直线方程代入椭圆方程,求得P的横坐标,求得丨BP丨,利用直线垂直的斜率关系求得丨BQ丨,由 ![]() =
= ![]() ,根据函数零点的判断即可存在k∈R,
,根据函数零点的判断即可存在k∈R, ![]() =
= ![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目