题目内容
【题目】已知函数f（x）=lnx﹣ax+ 
，其中a＞0．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）证明：（1+ 
）（1+ 
）（1+ 
）…（1+ 
）＜e 
（n∈N* ， n≥2）．
【答案】解：（Ⅰ）函数f（x）的定义域是（0，+∞）， f′（x）= 
，令h（x）=﹣ax2+x﹣a，
记△=1﹣4a2 ， 当△≤0时，得a≥ 
，
若a≥ ，则﹣ax2+x﹣a≤0，f′（x）≤0，
此时函数f（x）在（0，+∞）递减，
当0＜a＜ 时，由﹣ax2+x﹣a=0，解得：x1= 
，x2= 
，
显然x1＞x2＞0，故此时函数f（x）在（ ， ）递增，
在（0， ）和（ ，+∞）递减；
综上，0＜a＜ 时，函数f（x）在（ ， ）递增，
在（0， ）和（ ，+∞）递减，
a≥ 时，函数f（x）在（0，+∞）递减；
（Ⅱ）证明：令a= ，由（Ⅰ）中讨论可得函数f（x）在区间（0，+∞）递减，
又f（1）=0，从而当x∈（1，+∞）时，有f（x）＜0，即lnx＜ x﹣ 
，
令x=1+ 
（n≥2），
则ln（1+ ）＜ （1+ ）﹣ 
= 
= （ + 
）＜ 
= （ 
﹣ 
），
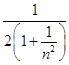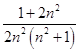
从而：ln（1+ 
）+ln（1+ 
）+ln（1+ 
）+…+ln（1+ ）
＜ （1﹣ 
+ ﹣ 
+ ﹣ 
+…+ 
﹣ + 
﹣ 
+ ﹣ ）
= （1+ ﹣ ﹣ ）＜ （1+ ）= 
，
则有ln（1+ ）+ln（1+ ）+ln（1+ ）+…+ln（1+ ）＜ ，
可得（1+ ）（1+ ）（1+ ）…（1+ ）＜e 
（n∈N* ， n≥2）
【解析】（Ⅰ）求出函数的导数，通过讨论a的范围，求出函数的单调区间即可；（Ⅱ）求出lnx＜ 
x﹣ 
，令x=1+ 
（n≥2），得到ln（1+ ）＜ （ 
﹣ 
），累加即可证明结论．
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减；求函数在
上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．
